Searching for a weak signal at an unknown frequency is a canonical task in experiments probing fundamental physics such as gravitational-wave observatories and ultra-light dark matter haloscopes. These state-of-the-art sensors are limited by quantum noise arising from the fundamental uncertainty about the state of the device. Classically, frequency estimation suffers from a threshold effect in the signal-to-noise ratio such that weak signals are extremely hard to localise in frequency. We show that this phenomenon persists at the fundamental quantum limit but that the classical approach, a quadrature measurement, can nevertheless be beaten by a coherent protocol of projecting onto the "quantum whitened" possible quantum states. Quantum whitening is a covariant measurement, and we examine it analytically in the wide-prior limit and numerically for finite-width priors. Beyond accelerating searches for unknown frequencies, quantum whitening may be used generally to sense the parameter of a unitary encoding given no prior information about the parameter. less

In this work, we examine the onset of thermodynamic chaos in Hayward AdS black holes with string fluids, emphasizing the effects of temporal and spatially periodic perturbations. We apply Melnikov's approach to examine the perturbed Hamiltonian dynamics and detect the onset of chaotic behavior within the spinodal regime of the $(P-v)$ plot. In the case of temporal perturbations induced by thermal quenches, chaos occurs for perturbation amplitude $\gamma$ exceeding a critical threshold that can be determined by charge $q$ and the string fluid parameter. From the equation of state of the black hole, a general condition can be established indicating that under temporal perturbations, the existence of charge is an essential prerequisite for chaos. In this regime, neutral Hayward black holes do not exhibit chaotic dynamics. However, regardless of the presence of charge, spatial perturbations result in chaotic behavior. The nonlinear interplay between the regularized core geometry and string fluids drives the formation of homoclinic and heteroclinic orbits in phase space, validating the persistence of chaos. The results obtained in this work, highlights the role of nonlinear matter fields and curvature regularization mechanisms in governing thermodynamic instability and the onset of chaos in Hayward black holes in AdS. less

Access control is a cornerstone of computer security that prevents unauthorised access to resources. In this paper, we study access control in quantum computer systems. We present the first explicit scenario of a security breach when a classically secure access control system is straightforwardly adapted to the quantum setting. The breach is ultimately due to that quantum mechanics allows the phenomenon of entanglement and violates Mermin inequality, a multi-party variant of the celebrated Bell inequality. This reveals a threat from quantum entanglement to access control if existing computer systems integrate with quantum computing. To protect against such threat, we propose several new models of quantum access control, and rigorously analyse their security, flexibility and efficiency. less

In this work, we study field theoretic systems of a single axion-like field with linear potentials modulated by cosine terms, allegedly induced by non-perturbative instanton configurations. These systems are considered in expanding-Universe spacetime backgrounds (of Friedman-Lema$\hat{\rm i}$tre-Robertson-Walker type). Using a dynamical-system approach, we classify the various de-Sitter like (inflationary) vacua from the point of view of their stability, which depend on the values of the model parameters. In this respect, bifurcation points are found to be present for the various models under consideration. Part of the parameter space of the systems under consideration includes the running-vacuum (approximately) linear-axion monodromy potentials, considered in previous works by some of the authors, where inflation is induced by primordial gravitational-wave condensates. A particularly interesting case, corresponding to another part of the parameter space of the models, includes a series of stable de-Sitter vacua, which physically may correspond to a series of successive tunnelings of the system, via say non-perturbative effects, with a decreasing effective cosmological constant. Under certain values of the parameters, these successive tunnelings can reach a Minkowski spacetime, with zero value of the minimum of the axion potential. The situation is not dissimilar to the one of discrete inflation that arguably characterizes some minimal non-critical-string (Liouville) models of cosmology. Finally, for comparison, we also include in this article a dynamical-system study of standard axion-monodromy-modulated potentials characterizing some string/brane-compactification models of inflation. less

In this note the Hamiltonian formulation of four-dimensional gravity, in the Palatini-Cartan formalism, is recovered by elimination of an auxiliary field appearing as part of the connection. less

Quantum hardware rarely suffers equal amounts of bit-flip ($X$) and phase-flip ($Z$) errors; one type is often much more common than the other. A code that is ``bias-tailored'' can exploit this imbalance, lowering the fault-tolerance overhead. A complementary idea, called "single-shot" error correction, aims to recover from data errors and noisy measurements in a single round of stabilizer readout, avoiding slow repetition cycles. In this work, we combine these two ideas and build a hierarchy of new quantum codes. The full construction starts from the syndrome-encoded hypergraph product code and then tailors it to the dominant error type. The resulting code keeps the single-shot guarantee for every noise model while boosting the threshold whenever $X$ and $Z$ errors are asymmetric. By removing carefully chosen blocks of stabilizers we obtain two trimmed variants. The first, called the simplified code, cuts the physical-qubit count by $1/6$ and halves the number of stabilizer measurements, yet its minimum distance grows quadratically compared to the standard design and its biased noise threshold is unchanged. The second, called the reduced code, achieves the same hardware savings but trades away single-shot protection for purely $X$ or purely $Z$ noise; instead it remains single-shot under balanced, or depolarizing, noise. In settings where strongly biased noise is likely, either trimmed code offers a less resource-intensive alternative to the full construction. As a concrete illustration, we lift the two-dimensional XZZX surface code to a three-dimensional cubic lattice and show that this ``3D XZZX'' code is an explicit member of the simplified family. Taken together, these bias-tailored single-shot codes provide an adjustable set of code design alternatives, allowing tradeoffs between hardware overhead and noise types. less

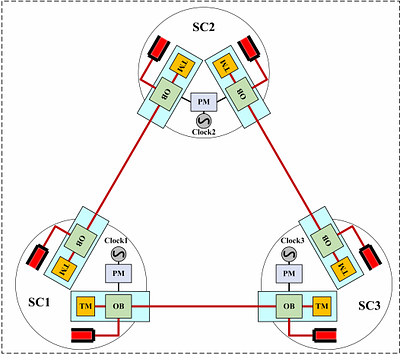
Space-borne gravitational wave detection will open the observation window in the 0.1 mHz$-$1 Hz bandwidth, playing a crucial role in the development of cosmology and physics. Precise clock synchronization among satellites is essential for the accurate detection of gravitational wave signals. However, the independent clock counting mechanisms of each satellite pose a significant challenge. This work reports the mathematical model of clock asynchrony, which is mainly dominated by the constant term factor and the linear term factor. Moreover, it experimentally verifies the clock asynchronization technique based on a dual-phasemeter system. Through experimentation, the impacts of these two aspects of clock asynchrony were confirmed, and post-processing techniques were employed to reduce these impacts to as low as $\rm 2\pi \times 10^{-6} rad/Hz^{1/2}@ 3mHz$. Specifically, the constant term factor is measured by Time-delay Interferometry Ranging (TDIR), while the linear term factor can be gauged by clock transmission link. This study provides a reference for understanding the clock asynchrony mechanism and processing clock synchronization issues. Additionally, a low additional noise clock synchronization test system is introduced to support such measurements. less

Cosmological production of scalar, non-minimally coupled dark matter depends on the specifics of the inflationary model under consideration. We analyze both Starobinsky inflation and a quadratic potential, solve the full background dynamics, study pair production during inflation and reheating, and find that the observed dark matter abundance can be explained solely by this mechanism, regardless of the inflationary model. Qualitative differences between the two cases only appear for dark matter masses close to the inflationary scale. In addition, we identify a large region in parameter space in which cosmological production of dark matter is mostly independent of the chosen inflationary potential, highlighting the robustness of this dark matter production mechanism and its independence of the unknown particular details of inflation. In the region of masses lower than the scale of inflation, and sufficiently away from the conformal limit, the total comoving number density of produced particles becomes a function of the coupling to the geometry alone. This allows us to provide an approximated analytic expression for fitting the resulting abundance. less

In earlier companion papers, we showed that non-singular primordial black holes (PBHs) could account for all the dark matter (DM) over a significantly wider mass range compared to Schwarzschild PBHs. Those studies, mostly based on phenomenological metrics, are now extended by considering the quantum-corrected space-time recently proposed by Zhang, Lewandowski, Ma and Yang (ZLMY), derived from an effective canonical (loop) quantum gravity approach explicitly enforcing general covariance. Unlike the BHs considered earlier, ZLMY BHs are free from Cauchy horizons, and are hotter than their Schwarzschild counterparts. We show that this higher temperature boosts the evaporation spectra of ZLMY PBHs, tightening limits on their abundance relative to Schwarzschild PBHs and shrinking the asteroid mass window where they can constitute all the DM, a result which reverses the earlier trend, but rests on firmer theoretical ground. While stressing the potential key role of quantum gravity effects in addressing the singularity and DM problems, our study shows that working within a consistent theoretical framework can strongly affect observational predictions. less

We introduce magic-augmented Clifford circuits -- architectures in which Clifford circuits are preceded and/or followed by constant-depth circuits of non-Clifford (``magic") gates -- as a resource-efficient way to realize approximate $k$-designs, with reduced circuit depth and usage of magic. We prove that shallow Clifford circuits, when augmented with constant-depth circuits of magic gates, can generate approximate unitary and state $k$-designs with $\epsilon$ relative error. The total circuit depth for these constructions on $N$ qubits is $O(\log (N/\epsilon)) +2^{O(k\log k)}$ in one dimension and $O(\log\log(N/\epsilon))+2^{O(k\log k)}$ in all-to-all circuits using ancillas, which improves upon previous results for small $k \geq 4$. Furthermore, our construction of relative-error state $k$-designs only involves states with strictly local magic. The required number of magic gates is parametrically reduced when considering $k$-designs with bounded additive error. As an example, we show that shallow Clifford circuits followed by $O(k^2)$ single-qubit magic gates, independent of system size, can generate an additive-error state $k$-design. We develop a classical statistical mechanics description of our random circuit architectures, which provides a quantitative understanding of the required depth and number of magic gates for additive-error state $k$-designs. We also prove no-go theorems for various architectures to generate designs with bounded relative error. less