In the field of Boolean satisfiability problems (SAT), at-most-k constraints, which suppress the number of true target variables at most k, are often used to describe objective problems. At-most-k constraints are used not only for absolutely necessary constraints (hard constraints) but also for challenging constraints (soft constraints) to search for better solutions. To encode at-most-k constraints into Boolean expressions, there is a problem that the number of Boolean expressions basically increases exponentially with the number of target variables, so at-most-k often has difficulties for a large number of variables. To solve this problem, this paper proposes a new encoding method of at-most-k constraints, called approximate-at-most-k, which has totally fewer Boolean expressions than conventional methods on the one hand. On the other hand, it has lost completeness, i.e., some Boolean value assignments that satisfy the original at-most-k are not allowed with approximate-at-most-k; hence, it is called approximate. Without completeness, we still have potential benefits by using them only as soft constraints. For example, approximate-at-most-16 out of 32 variables requires only 15% of a conventional at-most-k on the literal number and covers 44% of the solution space. Thus, approximate-at-most-k can become an alternative encoding method for at-most-k, especially as soft constraints. less

We present an approach to the verification of systems for whose description some elements - constants or functions - are underspecified and can be regarded as parameters, and, in particular, describe a method for automatically generating constraints on such parameters under which certain safety conditions are guaranteed to hold. We present an implementation and illustrate its use on several examples. less

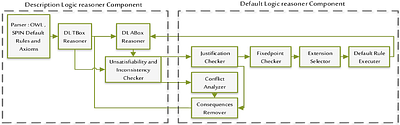
Prioritized Default Logic presents an optimal solution for addressing real-world problems characterized by incomplete information and the need to establish preferences among diverse scenarios. Although it has reached great success in the theoretical aspect, its practical implementation has received less attention. In this article, we introduce Borhan, a system designed and created for prioritized default logic reasoning. To create an effective system, we have refined existing default logic definitions, including the extension concept, and introduced novel concepts. In addition to its theoretical merits, Borhan proves its practical utility by efficiently addressing a range of prioritized default logic problems. In addition, one of the advantages of our system is its ability to both store and report the explanation path for any inferred triple, enhancing transparency and interpretability. Borhan is offered as an open-source system, implemented in Python, and even offers a simplified Java version as a plugin for the Protege ontology editor. Borhan thus represents a significant step forward in bridging the gap between the theoretical foundations of default logic and its real-world applications. less

We present MsATL: the first tool for deciding the satisfiability of Alternating-time Temporal Logic (ATL) with imperfect information. MsATL combines SAT Modulo Monotonic Theories solvers with existing ATL model checkers: MCMAS and STV. The tool can deal with various semantics of ATL, including perfect and imperfect information, and can handle additional practical requirements. MsATL can be applied for synthesis of games that conform to a given specification, with the synthesised game often being minimal. less

We investigate semiring provenance--a successful framework originally defined in the relational database setting--for description logics. In this context, the ontology axioms are annotated with elements of a commutative semiring and these annotations are propagated to the ontology consequences in a way that reflects how they are derived. We define a provenance semantics for a language that encompasses several lightweight description logics and show its relationships with semantics that have been defined for ontologies annotated with a specific kind of annotation (such as fuzzy degrees). We show that under some restrictions on the semiring, the semantics satisfies desirable properties (such as extending the semiring provenance defined for databases). We then focus on the well-known why-provenance, which allows to compute the semiring provenance for every additively and multiplicatively idempotent commutative semiring, and for which we study the complexity of problems related to the provenance of an axiom or a conjunctive query answer. Finally, we consider two more restricted cases which correspond to the so-called positive Boolean provenance and lineage in the database setting. For these cases, we exhibit relationships with well-known notions related to explanations in description logics and complete our complexity analysis. As a side contribution, we provide conditions on an ELHI_bot ontology that guarantee tractable reasoning. less

Logical frameworks can be used to translate proofs from a proof system to another one. For this purpose, we should be able to encode the theory of the proof system in the logical framework. The Lambda Pi calculus modulo theory is one of these logical frameworks. Powerful theories such as pure type systems with an infinite hierarchy of universes have been encoded, leading to partial encodings of proof systems such as Coq, Matita or Agda. In order to fully represent systems such as Coq and Lean, we introduce a representation of an infinite universe hierarchy with an impredicative universe and universe variables where universe equivalence is equality, and implement it as a terminating and confluent rewrite system. less

Non-fungible tokens, NFT, have been used to record ownership of real estate, art, digital assets, and more recently to serve legal notice. They provide an important and accessible non-financial use of cryptocurrency's blockchain but are peculiar because ownership by NFT confers no rights over the asset. This work shows that it is possible to specify that peculiar property by combining functional and epistemic properties. Suitability of the specification is evaluated by proof that the blockchain implementation conforms to it, and by its use in an analysis of serving legal notice. less

An automated resource analysis technique is introduced, targeting a Call-By-Push-Value abstract machine, with memory prediction as a practical goal. The machine has a polymorphic and linear type system enhanced with a first-order logical fragment, which encodes both low-level operational semantics of resource manipulations and high-level synthesis of algorithmic complexity. Resource analysis must involve a diversity of static analysis, for escape, aliasing, algorithmic invariants, and more. Knowing this, we implement the Automated Amortized Resource Analysis framework (AARA) from scratch in our generic system. In this setting, access to resources is a state-passing effect which produces a compile-time approximation of runtime resource usage. We implemented type inference constraint generation for our calculus, accompanied with an elaboration of bounds for iterators on algebraic datatypes, for minimal ML-style programming languages with Call-by-Value and Call-By-Push-Value semantics. The closed-formed bounds are derived as multivariate polynomials over the integers. This now serves as a base for the development of an experimental toolkit for automated memory analysis of functional languages. less

We introduce the class of P-finite automata. These are a generalisation of weighted automata, in which the weights of transitions can depend polynomially on the length of the input word. P-finite automata can also be viewed as simple tail-recursive programs in which the arguments of recursive calls can non-linearly refer to a variable that counts the number of recursive calls. The nomenclature is motivated by the fact that over a unary alphabet P-finite automata compute so-called P-finite sequences, that is, sequences that satisfy a linear recurrence with polynomial coefficients. Our main result shows that P-finite automata can be learned in polynomial time in Angluin's MAT exact learning model. This generalises the classical results that deterministic finite automata and weighted automata over a field are respectively polynomial-time learnable in the MAT model. less

The lambda-Pi-calculus allows to express proofs of minimal predicate logic. It can be extended, in a very simple way, by adding computation rules. This leads to the lambda-Pi-calculus modulo. We show in this paper that this simple extension is surprisingly expressive and, in particular, that all functional Pure Type Systems, such as the system F, or the Calculus of Constructions, can be embedded in it. And, moreover, that this embedding is conservative under termination hypothesis. less