By: Denis Cousineau LIX, Gilles Dowek
The lambda-Pi-calculus allows to express proofs of minimal predicate logic. It can be extended, in a very simple way, by adding computation rules. This leads to the lambda-Pi-calculus modulo. We show in this paper that this simple extension is surprisingly expressive and, in particular, that all functional Pure Type Systems, such as the system F, or the Calculus of Constructions, can be embedded in it. And, moreover, that this embedding is ... more
The lambda-Pi-calculus allows to express proofs of minimal predicate logic. It can be extended, in a very simple way, by adding computation rules. This leads to the lambda-Pi-calculus modulo. We show in this paper that this simple extension is surprisingly expressive and, in particular, that all functional Pure Type Systems, such as the system F, or the Calculus of Constructions, can be embedded in it. And, moreover, that this embedding is conservative under termination hypothesis. less
By: Javier Esparza, Rubén Rubio, Salomon Sickert
In the mid 80s, Lichtenstein, Pnueli, and Zuck proved a classical theorem stating that every formula of Past LTL (the extension of LTL with past operators) is equivalent to a formula of the form $\bigwedge_{i=1}^n \mathbf{G}\mathbf{F}\, \varphi_i \vee \mathbf{F}\mathbf{G}\, \psi_i $, where $\varphi_i$ and $\psi_i$ contain only past operators. Some years later, Chang, Manna, and Pnueli built on this result to derive a similar normal form for... more
In the mid 80s, Lichtenstein, Pnueli, and Zuck proved a classical theorem stating that every formula of Past LTL (the extension of LTL with past operators) is equivalent to a formula of the form $\bigwedge_{i=1}^n \mathbf{G}\mathbf{F}\, \varphi_i \vee \mathbf{F}\mathbf{G}\, \psi_i $, where $\varphi_i$ and $\psi_i$ contain only past operators. Some years later, Chang, Manna, and Pnueli built on this result to derive a similar normal form for LTL. Both normalization procedures have a non-elementary worst-case blow-up, and follow an involved path from formulas to counter-free automata to star-free regular expressions and back to formulas. We improve on both points. We present direct and purely syntactic normalization procedures for LTL, yielding a normal form very similar to the one by Chang, Manna, and Pnueli, that exhibit only a single exponential blow-up. As an application, we derive a simple algorithm to translate LTL into deterministic Rabin automata. The algorithm normalizes the formula, translates it into a special very weak alternating automaton, and applies a simple determinization procedure, valid only for these special automata. less
By: Enrique Matos Alfonso, Giorgos Stamou
In this paper, we explore conjunctive query rewriting, focusing on queries containing universally quantified negation within the framework of disjunctive existential rules. We address the undecidability of the existence of a finite and complete UCQ-rewriting and the identification of finite unification sets (fus) of rules. We introduce new rule classes, connected linear rules and connected domain restricted rules, that exhibit the fus prope... more
In this paper, we explore conjunctive query rewriting, focusing on queries containing universally quantified negation within the framework of disjunctive existential rules. We address the undecidability of the existence of a finite and complete UCQ-rewriting and the identification of finite unification sets (fus) of rules. We introduce new rule classes, connected linear rules and connected domain restricted rules, that exhibit the fus property for existential rules. Additionally, we propose disconnected disjunction for disjunctive existential rules to achieve the fus property when we extend the introduced rule fragments to disjunctive existential rules. We present ECOMPLETO, a system for efficient query rewriting with disjunctive existential rules, capable of handling UCQs with universally quantified negation. Our experiments demonstrate ECOMPLETO's consistent ability to produce finite UCQ-rewritings and describe the performance on different ontologies and queries. less
By: Andrew Craig, Claudette Robinson
We present a relational representation of odd Sugihara chains. The elements of the algebra are represented as weakening relations over a particular poset which consists of two densely embedded copies of the rationals. Our construction mimics that of Maddux (2010) where a relational representation of the even Sugihara chains is given. An order automorphism between the two copies of the rationals is the key to ensuring that the identity eleme... more
We present a relational representation of odd Sugihara chains. The elements of the algebra are represented as weakening relations over a particular poset which consists of two densely embedded copies of the rationals. Our construction mimics that of Maddux (2010) where a relational representation of the even Sugihara chains is given. An order automorphism between the two copies of the rationals is the key to ensuring that the identity element of the monoid is fixed by the involution. less
Arithmetic as a theory modulo
0upvotes
By: Gilles Dowek, Benjamin Werner
We present constructive arithmetic in Deduction modulo with rewrite rules only.
We present constructive arithmetic in Deduction modulo with rewrite rules only. less
Implicative models of set theory
0upvotes
By: Samuele Maschio, Alexandre Miquel
In this paper we show that using implicative algebras one can produce models of set theory generalizing Heyting/Boolean-valued models and realizability models of (I)ZF, both in intuitionistic and classical logic. This has as consequence that any topos which is obtained from a Set-based tripos as the result of the tripos-to-topos construction hosts a model of intuitionistic or classical set theory, provided a large enough strongly inaccessib... more
In this paper we show that using implicative algebras one can produce models of set theory generalizing Heyting/Boolean-valued models and realizability models of (I)ZF, both in intuitionistic and classical logic. This has as consequence that any topos which is obtained from a Set-based tripos as the result of the tripos-to-topos construction hosts a model of intuitionistic or classical set theory, provided a large enough strongly inaccessible cardinal exists. less
By: Roland Backhouse, Walter Guttmann, Michael Winter
We prove a non-trivial property of relations in a way that emphasises the creative process in its construction.
We prove a non-trivial property of relations in a way that emphasises the creative process in its construction. less
By: Aurore Alcolei, Luc Pellissier, Alexis Saurin
Linear logic has provided new perspectives on proof-theory, denotational semantics and the study of programming languages. One of its main successes are proof-nets, canonical representations of proofs that lie at the intersection between logic and graph theory. In the case of the minimalist proof-system of multiplicative linear logic without units (MLL), these two aspects are completely fused: proof-nets for this system are graphs satisfyin... more
Linear logic has provided new perspectives on proof-theory, denotational semantics and the study of programming languages. One of its main successes are proof-nets, canonical representations of proofs that lie at the intersection between logic and graph theory. In the case of the minimalist proof-system of multiplicative linear logic without units (MLL), these two aspects are completely fused: proof-nets for this system are graphs satisfying a correctness criterion that can be fully expressed in the language of graphs. For more expressive logical systems (containing logical constants, quantifiers and exponential modalities), this is not completely the case. The purely graphical approach of proof-nets deprives them of any sequential structure that is crucial to represent the order in which arguments are presented, which is necessary for these extensions. Rebuilding this order of presentation - sequentializing the graph - is thus a requirement for a graph to be logical. Presentations and study of the artifacts ensuring that sequentialization can be done, such as boxes or jumps, are an integral part of researches on linear logic. Jumps, extensively studied by Faggian and di Giamberardino, can express intermediate degrees of sequentialization between a sequent calculus proof and a fully desequentialized proof-net. We propose to analyze the logical strength of jumps by internalizing them in an extention of MLL where axioms on a specific formula, the jumping formula, introduce constrains on the possible sequentializations. The jumping formula needs to be treated non-linearly, which we do either axiomatically, or by embedding it in a very controlled fragment of multiplicative-exponential linear logic, uncovering the exponential logic of sequentialization. less
By: Étienne André, Didier Lime, Olivier H. Roux
Ensuring the correctness of critical real-time systems, involving concurrent behaviors and timing requirements, is crucial. Timed automata extend finite-state automata with clocks, compared in guards and invariants with integer constants. Parametric timed automata (PTAs) extend timed automata with timing parameters. Parameter synthesis aims at computing dense sets of valuations for the timing parameters, guaranteeing a good behavior. Howeve... more
Ensuring the correctness of critical real-time systems, involving concurrent behaviors and timing requirements, is crucial. Timed automata extend finite-state automata with clocks, compared in guards and invariants with integer constants. Parametric timed automata (PTAs) extend timed automata with timing parameters. Parameter synthesis aims at computing dense sets of valuations for the timing parameters, guaranteeing a good behavior. However, in most cases, the emptiness problem for reachability (i.e., whether the emptiness of the parameter valuations set for which some location is reachable) is undecidable for PTAs and, as a consequence, synthesis procedures do not terminate in general, even for bounded parameters. In this paper, we introduce a parametric extrapolation, that allows us to derive an underapproximation in the form of linear constraints containing not only all the integer points ensuring reachability, but also all the (non-necessarily integer) convex combinations of these integer points, for general PTAs with a bounded parameter domain. We also propose two further algorithms synthesizing parameter valuations guaranteeing unavoidability, and preservation of the untimed behavior w.r.t. a reference parameter valuation, respectively. Our algorithms terminate and can output constraints arbitrarily close to the complete result. We demonstrate their applicability and efficiency using the tool Rom\'eo on two classical benchmarks. less
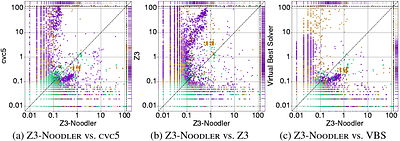
By: Yu-Fang Chen, David Chocholatý, Vojtěch Havlena, Lukáš Holík, Ondřej Lengál, Juraj Síč
Z3-Noodler is a fork of Z3 that replaces its string theory solver with a custom solver implementing the recently introduced stabilization-based algorithm for solving word equations with regular constraints. An extensive experimental evaluation shows that Z3-Noodler is a fully-fledged solver that can compete with state-of-the-art solvers, surpassing them by far on many benchmarks. Moreover, it is often complementary to other solvers, making ... more
Z3-Noodler is a fork of Z3 that replaces its string theory solver with a custom solver implementing the recently introduced stabilization-based algorithm for solving word equations with regular constraints. An extensive experimental evaluation shows that Z3-Noodler is a fully-fledged solver that can compete with state-of-the-art solvers, surpassing them by far on many benchmarks. Moreover, it is often complementary to other solvers, making it a suitable choice as a candidate to a solver portfolio. less