A Physics-Informed Neural Network (PINN) provides a distinct advantage by synergizing neural networks' capabilities with the problem's governing physical laws. In this study, we introduce an innovative approach for solving seepage problems by utilizing the PINN, harnessing the capabilities of Deep Neural Networks (DNNs) to approximate hydraulic head distributions in seepage analysis. To effectively train the PINN model, we introduce a comprehensive loss function comprising three components: one for evaluating differential operators, another for assessing boundary conditions, and a third for appraising initial conditions. The validation of the PINN involves solving four benchmark seepage problems. The results unequivocally demonstrate the exceptional accuracy of the PINN in solving seepage problems, surpassing the accuracy of FEM in addressing both steady-state and free-surface seepage problems. Hence, the presented approach highlights the robustness of the PINN and underscores its precision in effectively addressing a spectrum of seepage challenges. This amalgamation enables the derivation of accurate solutions, overcoming limitations inherent in conventional methods such as mesh generation and adaptability to complex geometries. less

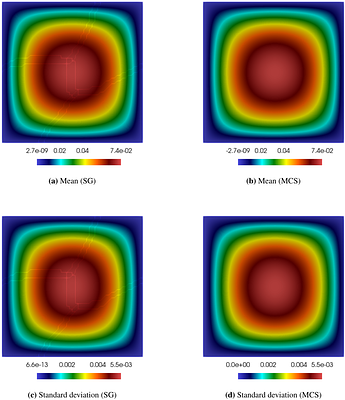
This article discusses the uncertainty quantification (UQ) for time-independent linear and nonlinear partial differential equation (PDE)-based systems with random model parameters carried out using sampling-free intrusive stochastic Galerkin method leveraging multilevel scalable solvers constructed combining two-grid Schwarz method and AMG. High-resolution spatial meshes along with a large number of stochastic expansion terms increase the system size leading to significant memory consumption and computational costs. Domain decomposition (DD)-based parallel scalable solvers are developed to this end for linear and nonlinear stochastic PDEs. A generalized minimum residual (GMRES) iterative solver equipped with a multilevel preconditioner consisting of restricted additive Schwarz (RAS) for the fine grid and algebraic multigrid (AMG) for the coarse grid is constructed to improve scalability. Numerical experiments illustrate the scalabilities of the proposed solver for stochastic linear and nonlinear Poisson problems. less

Immersed boundary methods simplify mesh generation by embedding the domain of interest into an extended domain that is easy to mesh, introducing the challenge of dealing with cells that intersect the domain boundary. Combined with explicit time integration schemes, the finite cell method introduces a lower bound for the critical time step size. Explicit transient analyses commonly use the spectral element method due to its natural way of obtaining diagonal mass matrices through nodal lumping. Its combination with the finite cell method is called the spectral cell method. Unfortunately, a direct application of nodal lumping in the spectral cell method is impossible due to the special quadrature necessary to treat the discontinuous integrand inside the cut cells. We analyze an implicit-explicit (IMEX) time integration method to exploit the advantages of the nodal lumping scheme for uncut cells on one side and the unconditional stability of implicit time integration schemes for cut cells on the other. In this hybrid, immersed Newmark IMEX approach, we use explicit second-order central differences to integrate the uncut degrees of freedom that lead to a diagonal block in the mass matrix and an implicit trapezoidal Newmark method to integrate the remaining degrees of freedom (those supported by at least one cut cell). The immersed Newmark IMEX approach preserves the high-order convergence rates and the geometric flexibility of the finite cell method. We analyze a simple system of spring-coupled masses to highlight some of the essential characteristics of Newmark IMEX time integration. We then solve the scalar wave equation on two- and three-dimensional examples with significant geometric complexity to show that our approach is more efficient than state-of-the-art time integration schemes when comparing accuracy and runtime. less

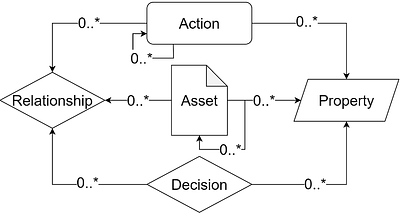
Industrial manufacturing is currently amidst it's fourth great revolution, pushing towards the digital transformation of production processes. One key element of this transformation is the formalization and digitization of processes, creating an increased potential to monitor, understand and optimize existing processes. However, one major obstacle in this process is the increased diversification and specialisation, resulting in the dependency on multiple experts, which are rarely amalgamated in small to medium sized companies. To mitigate this issue, this paper presents a novel approach for multi-criteria optimization of workflow-based assembly tasks in manufacturing by combining a workflow modeling framework and the HeuristicLab optimization framework. For this endeavour, a new generic problem definition is implemented in HeuristicLab, enabling the optimization of arbitrary workflows represented with the modeling framework. The resulting Pareto front of the multi-criteria optimization provides the decision makers a set of optimal workflows from which they can choose to optimally fit the current demands. The advantages of the herein presented approach are highlighted with a real world use case from an ongoing research project. less

Compliant mechanisms actuated by pneumatic loads are receiving increasing attention due to their direct applicability as soft robots that perform tasks using their flexible bodies. Using multiple materials to build them can further improve their performance and efficiency. Due to developments in additive manufacturing, the fabrication of multi-material soft robots is becoming a real possibility. To exploit this opportunity, there is a need for a dedicated design approach. This paper offers a systematic approach to developing such mechanisms using topology optimization. The extended SIMP scheme is employed for multi-material modeling. The design-dependent nature of the pressure load is modeled using the Darcy law with a volumetric drainage term. Flow coefficient of each element is interpolated using a smoothed Heaviside function. The obtained pressure field is converted to consistent nodal loads. The adjoint-variable approach is employed to determine the sensitivities. A robust formulation is employed, wherein a min-max optimization problem is formulated using the output displacements of the eroded and blueprint designs. Volume constraints are applied to the blueprint design, whereas the strain energy constraint is formulated with respect to the eroded design. The efficacy and success of the approach are demonstrated by designing pneumatically actuated multi-material gripper and contractor mechanisms. A numerical study confirms that multiple-material mechanisms perform relatively better than their single-material counterparts. less

We formulate and solve data-driven aerodynamic shape design problems with distributionally robust optimization (DRO) approaches. Building on the findings of the work \cite{gotoh2018robust}, we study the connections between a class of DRO and the Taguchi method in the context of robust design optimization. Our preliminary computational experiments on aerodynamic shape optimization in transonic turbulent flow show promising design results. less

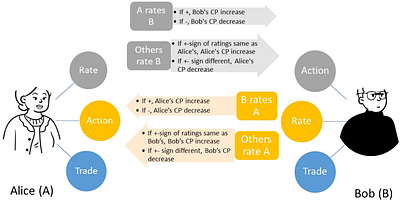
In the era of digital markets, the challenge for consumers is discerning quality amidst information asymmetry. While traditional markets use brand mechanisms to address this issue, transferring such systems to internet-based P2P markets, where misleading practices like fake ratings are rampant, remains challenging. Current internet platforms strive to counter this through verification algorithms, but these efforts find themselves in a continuous tug-of-war with counterfeit actions. Exploiting the transparency, immutability, and traceability of blockchain technology, this paper introduces a robust reputation voting system grounded in it. Unlike existing blockchain-based reputation systems, our model harnesses an intrinsically economically incentivized approach to bolster agent integrity. We optimize this model to mirror real-world user behavior, preserving the reputation system's foundational sustainability. Through Monte-Carlo simulations, using both uniform and power-law distributions enabled by an innovative inverse transform method, we traverse a broad parameter landscape, replicating real-world complexity. The findings underscore the promise of a sustainable, transparent, and formidable reputation mechanism. Given its structure, our framework can potentially function as a universal, sustainable oracle for offchain-onchain bridging, aiding entities in perpetually cultivating their reputation. Future integration with technologies like Ring Signature and Zero Knowledge Proof could amplify the system's privacy facets, rendering it particularly influential in the ever-evolving digital domain. less

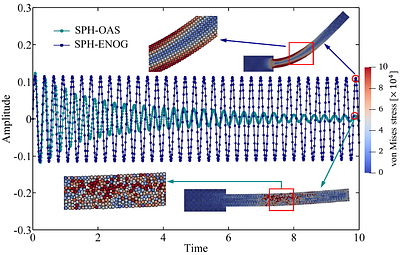
Since the tension instability was discovered in updated Lagrangian smoothed particle hydrodynamics (ULSPH) at the end of the 20th century, researchers have made considerable efforts to suppress its occurrence. However, up to the present day, this problem has not been fundamentally resolved. In this paper, the concept of hourglass modes is firstly introduced into ULSPH, and the inherent causes of tension instability in elastic dynamics are clarified based on this brand-new perspective. Specifically, we present an essentially non-hourglass formulation by decomposing the shear acceleration with the Laplacian operator, and a comprehensive set of challenging benchmark cases for elastic dynamics is used to showcase that our method can completely eliminate tensile instability by resolving hourglass modes. The present results reveal the true origin of tension instability and challenge the traditional understanding of its sources, i.e., hourglass modes are the real culprit behind inducing this instability in tension zones rather that the tension itself. Furthermore, a time integration scheme known as dual-criteria time stepping is adopted into the simulation of solids for the first time, to significantly enhance computational efficiency. less

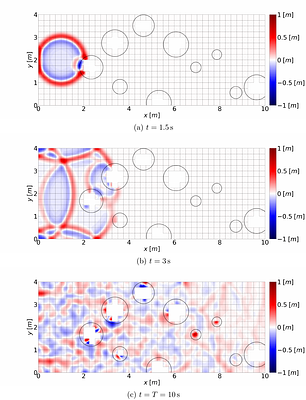
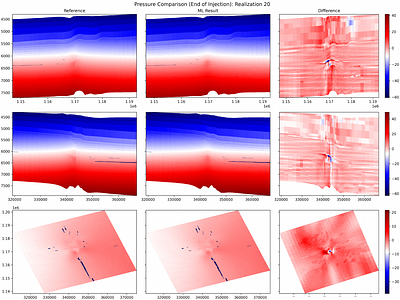
Geological carbon and energy storage are pivotal for achieving net-zero carbon emissions and addressing climate change. However, they face uncertainties due to geological factors and operational limitations, resulting in possibilities of induced seismic events or groundwater contamination. To overcome these challenges, we propose a specialized machine-learning (ML) model to manage extensive reservoir models efficiently. While ML approaches hold promise for geological carbon storage, the substantial computational resources required for large-scale analysis are the obstacle. We've developed a method to reduce the training cost for deep neural operator models, using domain decomposition and a topology embedder to link spatio-temporal points. This approach allows accurate predictions within the model's domain, even for untrained data, enhancing ML efficiency for large-scale geological storage applications. less

Artificial intelligence holds promise to improve materials discovery. GFlowNets are an emerging deep learning algorithm with many applications in AI-assisted discovery. By using GFlowNets, we generate porous reticular materials, such as metal organic frameworks and covalent organic frameworks, for applications in carbon dioxide capture. We introduce a new Python package (matgfn) to train and sample GFlowNets. We use matgfn to generate the matgfn-rm dataset of novel and diverse reticular materials with gravimetric surface area above 5000 m$^2$/g. We calculate single- and two-component gas adsorption isotherms for the top-100 candidates in matgfn-rm. These candidates are novel compared to the state-of-art ARC-MOF dataset and rank in the 90th percentile in terms of working capacity compared to the CoRE2019 dataset. We discover 15 materials outperforming all materials in CoRE2019. less