We prove that a polynomial fraction of the set of $k$-component forests in the $m \times n$ grid graph have equal numbers of vertices in each component. This resolves a conjecture of Charikar, Liu, Liu, and Vuong. It also establishes the first provably polynomial-time algorithm for (exactly or approximately) sampling balanced grid graph partitions according to the spanning tree distribution, which weights each $k$-partition according to the product, across its $k$ pieces, of the number of spanning trees of each piece. Our result has applications to understanding political districtings, where there is an underlying graph of indivisible geographic units that must be partitioned into $k$ population-balanced connected subgraphs. In this setting, tree-weighted partitions have interesting geometric properties, and this has stimulated significant effort to develop methods to sample them. less

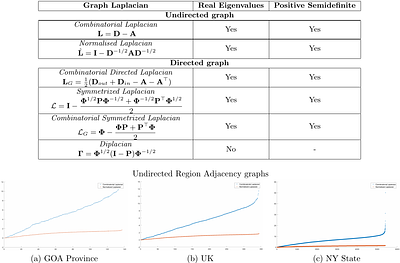
Urban mobility forecast and analysis can be addressed through grid-based and graph-based models. However, graph-based representations have the advantage of more realistically depicting the mobility networks and being more robust since they allow the implementation of Graph Theory machinery, enhancing the analysis and visualisation of mobility flows. We define two types of mobility graphs: Region Adjacency graphs and Origin-Destination graphs. Several node centrality metrics of graphs are applied to identify the most relevant nodes of the network in terms of graph connectivity. Additionally, the Perron vector associated with a strongly connected graph is applied to define a circulation function on the mobility graph. Such node values are visualised in the geographically embedded graphs, showing clustering patterns within the network. Since mobility graphs can be directed or undirected, we define several Graph Laplacian for both cases and show that these matrices and their spectral properties provide insightful information for network analysis. The computation of node centrality metrics and Perron-induced circulation functions for three different geographical regions demonstrate that basic elements from Graph Theory applied to mobility networks can lead to structure analysis for graphs of different connectivity, size, and orientation properties. less

A connected matching in a graph G consists of a set of pairwise disjoint edges whose covered vertices induce a connected subgraph of G. While finding a connected matching of maximum cardinality is a well-solved problem, it is NP-hard to determine an optimal connected matching in an edge-weighted graph, even in the planar bipartite case. We present two mixed integer programming formulations and a sophisticated branch-and-cut scheme to find weighted connected matchings in general graphs. The formulations explore different polyhedra associated to this problem, including strong valid inequalities both from the matching polytope and from the connected subgraph polytope. We conjecture that one attains a tight approximation of the convex hull of connected matchings using our strongest formulation, and report encouraging computational results over DIMACS Implementation Challenge benchmark instances. The source code of the complete implementation is also made available. less

The Integer Multicommodity Flow problem has been studied extensively in the literature. However, from a parameterised perspective, mostly special cases, such as the Disjoint Paths problem, have been considered. Therefore, we investigate the parameterised complexity of the general Integer Multicommodity Flow problem. We show that the decision version of this problem on directed graphs for a constant number of commodities, when the capacities are given in unary, is XNLP-complete with pathwidth as parameter and XALP-complete with treewidth as parameter. When the capacities are given in binary, the problem is NP-complete even for graphs of pathwidth at most 13. We give related results for undirected graphs. These results imply that the problem is unlikely to be fixed-parameter tractable by these parameters. In contrast, we show that the problem does become fixed-parameter tractable when weighted tree partition width (a variant of tree partition width for edge weighted graphs) is used as parameter. less

Mixed Hamming packings are considered: the maximal cardinality given a minimum codeword Hamming distance of mixed codes is addressed via mixed integer programming models. Adopting the concept of contact graph from classical continuous sphere packing problems, a reduction technique for the models is introduced, which enables their efficient solution. Several best known upper bounds are improved and some of them are found to be sharp. less

Problems from metric graph theory such as Metric Dimension, Geodetic Set, and Strong Metric Dimension have recently had a strong impact on the field of parameterized complexity by being the first problems in NP to admit double-exponential lower bounds in the treewidth, and even in the vertex cover number for the latter. We initiate the study of enumerating minimal solution sets for these problems and show that they are also of great interest in enumeration. More specifically, we show that enumerating minimal resolving sets in graphs and minimal geodetic sets in split graphs are equivalent to hypergraph dualization, arguably one of the most important open problems in algorithmic enumeration. This provides two new natural examples to a question that emerged in different works this last decade: for which vertex (or edge) set graph property $\Pi$ is the enumeration of minimal (or maximal) subsets satisfying $\Pi$ equivalent to hypergraph dualization? As only very few properties are known to fit within this context -- namely, properties related to minimal domination -- our results make significant progress in characterizing such properties, and provide new angles of approach for tackling hypergraph dualization. In a second step, we consider cases where our reductions do not apply, namely graphs with no long induced paths, and show these cases to be mainly tractable. less

The support of a flow $x$ in a network is the subdigraph induced by the arcs $ij$ for which $x_{ij}>0$. We discuss a number of results on flows in networks where we put certain restrictions on structure of the support of the flow. Many of these problems are NP-hard because they generalize linkage problems for digraphs. For example deciding whether a network ${\cal N}=(D,s,t,c)$ has a maximum flow $x$ such that the maximum out-degree of the support $D_x$ of $x$ is at most 2 is NP-complete as it contains the 2-linkage problem as a very special case. Another problem which is NP-complete for the same reason is that of deciding the maximum flow we can send from $s$ to $t$ along 2 paths (called a maximum 2-path-flow) in ${\cal N}$. Baier et al. (2005) gave a polynomial algorithm which finds a 2-path-flow $x$ whose value is at least $\frac{2}{3}$ of the value of a optimum 2-path-flow. This is best possible unless P=NP. They also obtained a $\frac{2}{p}$-approximation for the maximum value of a $p$-path-flow for every $p\geq 2$. In this paper we give an algorithm which gets within a factor $\frac{1}{H(p)}$ of the optimum solution, where $H(p)$ is the $p$'th harmonic number ($H(p) \sim \ln(p)$). This improves the approximation bound due to Baier et al. when $p\geq 5$. We show that in the case where the network is acyclic, we can find a maximum $p$-path-flow in polynomial time for every $p$. We determine the complexity of a number of related problems concerning the structure of flows. For the special case of acyclic digraphs, some of the results we obtain are in some sense best possible. less