We initiate the study of sub-linear sketching and streaming techniques for estimating the output size of common dictionary compressors such as Lempel-Ziv '77, the run-length Burrows-Wheeler transform, and grammar compression. To this end, we focus on a measure that has recently gained much attention in the information-theoretic community and which approximates up to a polylogarithmic multiplicative factor the output sizes of those compressors: the normalized substring complexity function $\delta$. As a matter of fact, $\delta$ itself is a very accurate measure of compressibility: it is monotone under concatenation, invariant under reversals and alphabet permutations, sub-additive, and asymptotically tight (in terms of worst-case entropy) for representing strings, up to polylogarithmic factors. We present a data sketch of $O(\epsilon^{-3}\log n + \epsilon^{-1}\log^2 n)$ words that allows computing a multiplicative $(1\pm \epsilon)$-approximation of $\delta$ with high probability, where $n$ is the string length. The sketches of two strings $S_1,S_2$ can be merged in $O(\epsilon^{-1}\log^2 n)$ time to yield the sketch of $\{S_1,S_2\}$, speeding up by orders of magnitude tasks such as the computation of all-pairs \emph{Normalized Compression Distances} (NCD). If random access is available on the input, our sketch can be updated in $O(\epsilon^{-1}\log^2 n)$ time for each character right-extension of the string. This yields a polylogarithmic-space algorithm for approximating $\delta$, improving exponentially over the working space of the state-of-the-art algorithms running in nearly-linear time. Motivated by the fact that random access is not always available on the input data, we then present a streaming algorithm computing our sketch in $O(\sqrt n \cdot \log n)$ working space and $O(\epsilon^{-1}\log^2 n)$ worst-case delay per character. less

In this paper, we study the Min-cost Perfect $k$-way Matching with Delays ($k$-MPMD), recently introduced by Melnyk et al. In the problem, $m$ requests arrive one-by-one over time in a metric space. At any time, we can irrevocably make a group of $k$ requests who arrived so far, that incurs the distance cost among the $k$ requests in addition to the sum of the waiting cost for the $k$ requests. The goal is to partition all the requests into groups of $k$ requests, minimizing the total cost. The problem is a generalization of the min-cost perfect matching with delays (corresponding to $2$-MPMD). It is known that no online algorithm for $k$-MPMD can achieve a bounded competitive ratio in general, where the competitive ratio is the worst-case ratio between its performance and the offline optimal value. On the other hand, $k$-MPMD is known to admit a randomized online algorithm with competitive ratio $O(k^{5}\log n)$ for a certain class of $k$-point metrics called the $H$-metric, where $n$ is the size of the metric space. In this paper, we propose a deterministic online algorithm with a competitive ratio of $O(mk^2)$ for the $k$-MPMD in $H$-metric space. Furthermore, we show that the competitive ratio can be improved to $O(m + k^2)$ if the metric is given as a diameter on a line. less

We give improved algorithms for maintaining edge-orientations of a fully-dynamic graph, such that the maximum out-degree is bounded. On one hand, we show how to orient the edges such that maximum out-degree is proportional to the arboricity $\alpha$ of the graph, in, either, an amortised update time of $O(\log^2 n \log \alpha)$, or a worst-case update time of $O(\log^3 n \log \alpha)$. On the other hand, motivated by applications including dynamic maximal matching, we obtain a different trade-off. Namely, the improved update time of either $O(\log n \log \alpha)$, amortised, or $O(\log ^2 n \log \alpha)$, worst-case, for the problem of maintaining an edge-orientation with at most $O(\alpha + \log n)$ out-edges per vertex. Finally, all of our algorithms naturally limit the recourse to be polylogarithmic in $n$ and $\alpha$. Our algorithms adapt to the current arboricity of the graph. Moreover, further analysis shows that they can yield a $(1 + \varepsilon)$-approximation of the arboricity or the subgraph density at the cost of increased update time. less

We develop a general framework for finding approximately-optimal preconditioners for solving linear systems. Leveraging this framework we obtain improved runtimes for fundamental preconditioning and linear system solving problems including the following. We give an algorithm which, given positive definite $\mathbf{K} \in \mathbb{R}^{d \times d}$ with $\mathrm{nnz}(\mathbf{K})$ nonzero entries, computes an $\epsilon$-optimal diagonal preconditioner in time $\widetilde{O}(\mathrm{nnz}(\mathbf{K}) \cdot \mathrm{poly}(\kappa^\star,\epsilon^{-1}))$, where $\kappa^\star$ is the optimal condition number of the rescaled matrix. We give an algorithm which, given $\mathbf{M} \in \mathbb{R}^{d \times d}$ that is either the pseudoinverse of a graph Laplacian matrix or a constant spectral approximation of one, solves linear systems in $\mathbf{M}$ in $\widetilde{O}(d^2)$ time. Our diagonal preconditioning results improve state-of-the-art runtimes of $\Omega(d^{3.5})$ attained by general-purpose semidefinite programming, and our solvers improve state-of-the-art runtimes of $\Omega(d^{\omega})$ where $\omega > 2.3$ is the current matrix multiplication constant. We attain our results via new algorithms for a class of semidefinite programs (SDPs) we call matrix-dictionary approximation SDPs, which we leverage to solve an associated problem we call matrix-dictionary recovery. less

We present a $O(1)$-approximate fully dynamic algorithm for the $k$-median and $k$-means problems on metric spaces with amortized update time $\tilde O(k)$ and worst-case query time $\tilde O(k^2)$. We complement our theoretical analysis with the first in-depth experimental study for the dynamic $k$-median problem on general metrics, focusing on comparing our dynamic algorithm to the current state-of-the-art by Henzinger and Kale [ESA'20]. Finally, we also provide a lower bound for dynamic $k$-median which shows that any $O(1)$-approximate algorithm with $\tilde O(\text{poly}(k))$ query time must have $\tilde \Omega(k)$ amortized update time, even in the incremental setting. less

Listing copies of small subgraphs (such as triangles, $4$-cycles, small cliques) in the input graph is an important and well-studied problem in algorithmic graph theory. In this paper, we give a simple algorithm that lists $t$ (non-induced) $6$-cycles in an $n$-node undirected graph in $\tilde O(n^2+t)$ time. This nearly matches the fastest known algorithm for detecting a $6$-cycle in $O(n^2)$ time by Yuster and Zwick (1997). Previously, a folklore $O(n^2+t)$-time algorithm was known for the task of listing $4$-cycles. less

Traditionally in the turnstile model of data streams, there is a state vector $x=(x_1,x_2,\ldots,x_n)$ which is updated through a stream of pairs $(i,k)$ where $i\in [n]$ and $k\in \Z$. Upon receiving $(i,k)$, $x_i\gets x_i + k$. A distinct count algorithm in the turnstile model takes one pass of the stream and then estimates $\norm{x}_0 = |\{i\in[n]\mid x_i\neq 0\}|$ (aka $L_0$, the Hamming norm). In this paper, we define a finite-field version of the turnstile model. Let $F$ be any finite field. Then in the $F$-turnstile model, for each $i\in [n]$, $x_i\in F$; for each update $(i,k)$, $k\in F$. The update $x_i\gets x_i+k$ is then computed in the field $F$. A distinct count algorithm in the $F$-turnstile model takes one pass of the stream and estimates $\norm{x}_{0;F} = |\{i\in[n]\mid x_i\neq 0_F\}|$. We present a simple distinct count algorithm, called $F$-\pcsa{}, in the $F$-turnstile model for any finite field $F$. The new $F$-\pcsa{} algorithm takes $m\log(n)\log (|F|)$ bits of memory and estimates $\norm{x}_{0;F}$ with $O(\frac{1}{\sqrt{m}})$ relative error where the hidden constant depends on the order of the field. $F$-\pcsa{} is straightforward to implement and has several applications in the real world with different choices of $F$. Most notably, it makes distinct count with deletions as simple as distinct count without deletions. less

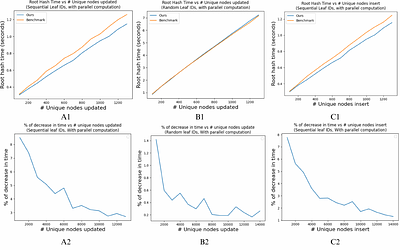
A sparse Merkle tree is a Merkle tree with fixed height and indexed leaves given by a map from indices to leaf values. It allows for both efficient membership and non-membership proofs. It has been widely used as an authenticated data structure in various applications, such as layer-2 rollups for blockchains. zkSync Lite, a popular Ethereum layer-2 rollup solution, uses a sparse Merkle tree to represent the state of the layer-2 blockchain. The account information is recorded in the leaves of the tree. In this paper, we study the sparse Merkle tree algorithms presented in zkSync Lite, and propose an efficient batch update algorithm to calculate a new root hash given a list of account (leaf) operations. Using the construction in zkSync Lite as a benchmark, our algorithm 1) improves the account update time from $\mathcal{O}(\log n)$ to $\mathcal{O}(1)$ and 2) reduces the batch update cost by half using a one-pass traversal. Empirical analysis of real-world block data shows that our algorithm outperforms the benchmark by at most 14%. less

Metarounding is an approach to convert an approximation algorithm for linear optimization over some combinatorial classes to an online linear optimization algorithm for the same class. We propose a new metarounding algorithm under a natural assumption that a relax-based approximation algorithm exists for the combinatorial class. Our algorithm is much more efficient in both theoretical and practical aspects. less

Connectivity (or equivalently, unweighted maximum flow) is an important measure in graph theory and combinatorial optimization. Given a graph $G$ with vertices $s$ and $t$, the connectivity $\lambda(s,t)$ from $s$ to $t$ is defined to be the maximum number of edge-disjoint paths from $s$ to $t$ in $G$. Much research has gone into designing fast algorithms for computing connectivities in graphs. Previous work showed that it is possible to compute connectivities for all pairs of vertices in directed graphs with $m$ edges in $\tilde{O}(m^\omega)$ time [Chueng, Lau, and Leung, FOCS 2011], where $\omega \in [2,2.3716)$ is the exponent of matrix multiplication. For the related problem of computing "small connectivities," it was recently shown that for any positive integer $k$, we can compute $\min(k,\lambda(s,t))$ for all pairs of vertices $(s,t)$ in a directed graph with $n$ nodes in $\tilde{O}((kn)^\omega)$ time [Akmal and Jin, ICALP 2023]. In this paper, we present an alternate exposition of these $\tilde{O}(m^\omega)$ and $\tilde{O}((kn)^\omega)$ time algorithms, with simpler proofs of correctness. Earlier proofs were somewhat indirect, introducing an elegant but ad hoc "flow vector framework" for showing correctness of these algorithms. In contrast, we observe that these algorithms for computing exact and small connectivity values can be interpreted as testing whether certain generating functions enumerating families of edge-disjoint paths are nonzero. This new perspective yields more transparent proofs, and ties the approach for these problems more closely to the literature surrounding algebraic graph algorithms. less