Jagadeesan, P.; Raman, K.; Tangirala, A. K.

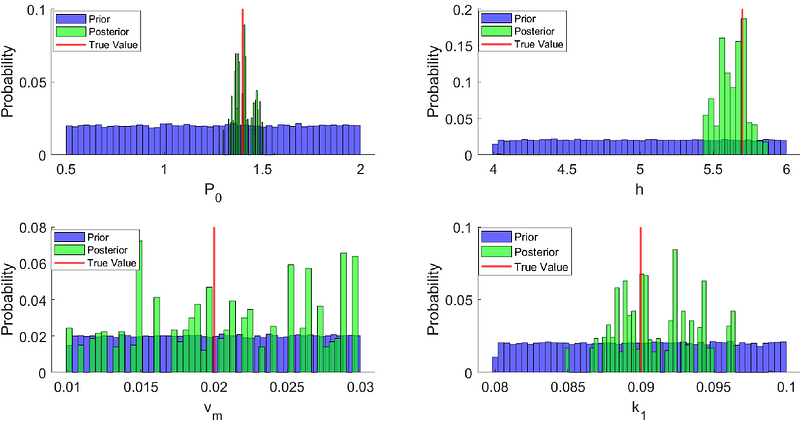
Computational modelling of dynamical systems often involves many free parameters estimated from experimental data. The information gained from an experiment plays a crucial role in the goodness of predictions and parameter estimates. Optimal Experiment Design (OED) is being used to choose an experiment containing maximum information from a set of possible experiments. This work presents a novel Bayesian Optimal Experiment Design principle for generalised parameter distributions. The generalization is archived by extending the {beta}-information gain to the discrete distributions. The {beta}-information gain is based on what is known as the Bhattacharyya coefficient. We show that maximising the {beta}-information gain is equivalent to maximising the angle between the prior and posterior distributions, reducing the posterior\'s uncertainty. Further, we apply the proposed BOED criteria for two realistic experiment designs in systems biology. Firstly, we use the {beta}-information gain to choose the best measurement method for parameter estimation in a Hes1 transcription model. The measurement method selected by the {beta}-information gain results in the minimum mean square error of the parameter estimates. In the second case, we employ the proposed information gained to select an optimal sampling schedule for HIV 1 2 LTR model. The sampling schedule chosen by the presented method reduces both prediction and parameter uncertainty. Finally, we propose a novel method for model selection using {beta}-information gain and demonstrate the working of the proposed method in the model selection in compartmental models.