By: Sofía González-García, Aaron Szasz, Alice Pagano, Dvir Kafri, Guifré Vidal, Agustin Di Paolo
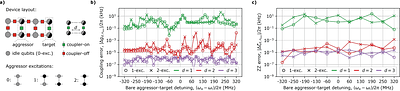
Obtaining accurate representations of the eigenstates of an array of coupled superconducting qubits is a crucial step in the design of circuit quantum electrodynamics (QED)-based quantum processors. However, exact diagonalization of the device Hamiltonian is challenging for system sizes beyond tens of qubits. Here, we employ a variant of the density matrix renormalization group (DMRG) algorithm, DMRG-X, to efficiently obtain localized eigenst... more
Obtaining accurate representations of the eigenstates of an array of coupled superconducting qubits is a crucial step in the design of circuit quantum electrodynamics (QED)-based quantum processors. However, exact diagonalization of the device Hamiltonian is challenging for system sizes beyond tens of qubits. Here, we employ a variant of the density matrix renormalization group (DMRG) algorithm, DMRG-X, to efficiently obtain localized eigenstates of a 2D transmon array without the need to first compute lower-energy states. We also introduce MTDMRG-X, a new algorithm that combines DMRG-X with multi-target DMRG to efficiently compute excited states even in regimes with strong eigenstate hybridization. We showcase the use of these methods for the analysis of long-range couplings in a multi-transmon Hamiltonian including qubits and couplers, and we discuss eigenstate localization. These developments facilitate the design and parameter optimization of large-scale superconducting quantum processors. less
By: Ryotaro Niwa, Zane Marius Rossi, Philip Taranto, Mio Murao
Given the ability to apply an unknown quantum channel acting on a $d$-dimensional system, we develop a quantum algorithm for transforming its singular values. The spectrum of a quantum channel as a superoperator is naturally tied to its Liouville representation, which is in general non-Hermitian. Our key contribution is an approximate block-encoding scheme for this representation in a Hermitized form, given only black-box access to the channe... more
Given the ability to apply an unknown quantum channel acting on a $d$-dimensional system, we develop a quantum algorithm for transforming its singular values. The spectrum of a quantum channel as a superoperator is naturally tied to its Liouville representation, which is in general non-Hermitian. Our key contribution is an approximate block-encoding scheme for this representation in a Hermitized form, given only black-box access to the channel; this immediately allows us to apply polynomial transformations to the channel's singular values by quantum singular value transformation (QSVT). We then demonstrate an $O(d^2/\delta)$ upper bound and an $\Omega(d/\delta)$ lower bound for the query complexity of constructing a quantum channel that is $\delta$-close in diamond norm to a block-encoding of the Hermitized Liouville representation. We show our method applies practically to the problem of learning the $q$-th singular value moments of unknown quantum channels for arbitrary $q>2, q\in \mathbb{R}$, which has implications for testing if a quantum channel is entanglement breaking. less
9 SciCasts by .