Aavishkar Madhunlall, Chevarra Hansraj, Rituparno Goswami, Sunil D. Maharaj

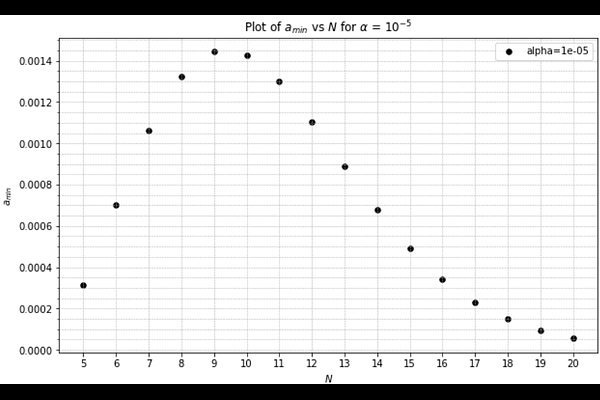
In this paper we study the higher dimensional homogeneous and isotropic perfect fluid spacetimes in Einstein-Gauss-Bonnet (EGB) gravity. We solve the modified field equations with higher order curvature terms to determine the evolution of the scale factor. We transparently show that this scale factor cannot become smaller than a finite minimum positive value which depends on the dimension and equation of state. This bound completely eliminates any curvature singularities in the spacetimes, where the scale factor must tend to zero. This is a unique property of EGB gravity which, despite being ghost-free and having quasi-linear field equations like general relativity, allows for the violation of singularity theorems. This phenomenon, thus, gives a natural way to dynamically construct regular black holes via higher dimensional continual gravitational collapse.