Claudio Lazarte, Nicolas Sanchis-Gual, José A. Font, Miguel Alcubierre

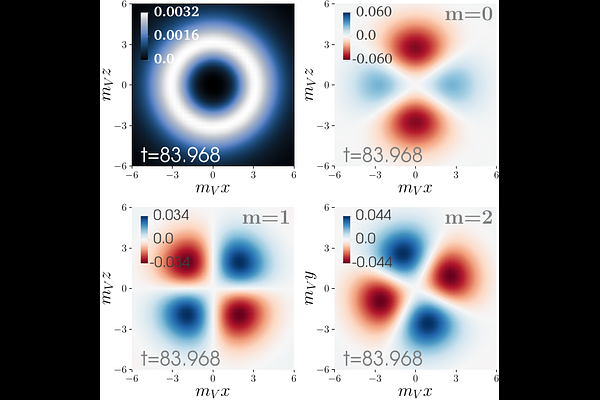
Vector boson stars, also known as Proca stars, exhibit remarkable dynamical robustness, making them strong candidates for potential astrophysical exotic compact objects. In search of theoretically well-motivated Proca star models, we recently introduced the $\ell$-Proca star, a multi-field extension of the spherical Proca star, whose $(2\ell + 1)$ constitutive fields have the same time and radial dependence, and their angular structure is given by all the available spherical harmonics for a fixed angular momentum number $\ell$. In this work, we conduct a non-linear stability analysis of these stars by numerically solving the Einstein-(multi, complex) Proca system for the case of $\ell = 2$, which are formed by five constitutive independent, complex Proca fields with $m = 0, |1|$, and $|2|$. Our analysis is based on long-term, fully non-linear, 3-dimensional numerical-relativity simulations without imposing any symmetry. We find that ($\ell=2$)-Proca stars are unstable throughout their entire domain of existence. In particular, we highlight that less compact configurations dynamically lose their global spherical symmetry, developing a non-axisymmetric $\tilde{m}=4$ mode instability and a subsequent migration into a new kind of multi-field Proca star formed by fields with different angular momentum number, $\ell=1$ and $\ell=2$, that we identify as unstable multi-$\ell$ Proca stars.