Sabri Meyer, Francesco Scala, Francesco Tacchino, Aurelien Lucchi

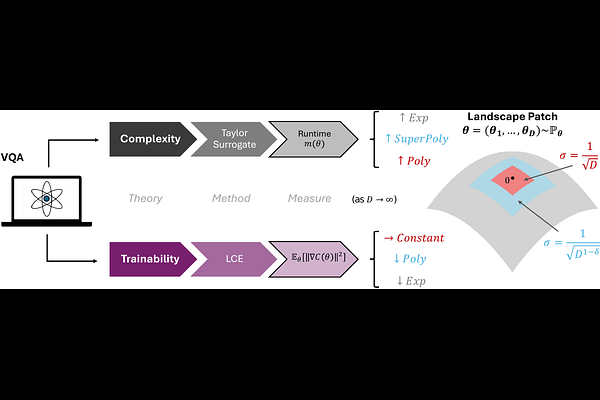
Variational Quantum Algorithms (VQAs) are promising candidates for near-term quantum computing, yet they face scalability challenges due to barren plateaus, where gradients vanish exponentially in the system size. Recent conjectures suggest that avoiding barren plateaus might inherently lead to classical simulability, thus limiting the opportunities for quantum advantage. In this work, we advance the theoretical understanding of the relationship between the trainability and computational complexity of VQAs, thus directly addressing the conjecture. We introduce the Linear Clifford Encoder (LCE), a novel technique that ensures constant-scaling gradient statistics on optimization landscape regions that are close to Clifford circuits. Additionally, we leverage classical Taylor surrogates to reveal computational complexity phase transitions from polynomial to super-polynomial as the initialization region size increases. Combining these results, we reveal a deeper link between trainability and computational complexity, and analytically prove that barren plateaus can be avoided in regions for which no classical surrogate is known to exist. Furthermore, numerical experiments on LCE transformed landscapes confirm in practice the existence of a super-polynomially complex ``transition zone'' where gradients decay polynomially. These findings indicate a plausible path to practically relevant, barren plateau-free variational models with potential for quantum advantage.