Marcin Postolak

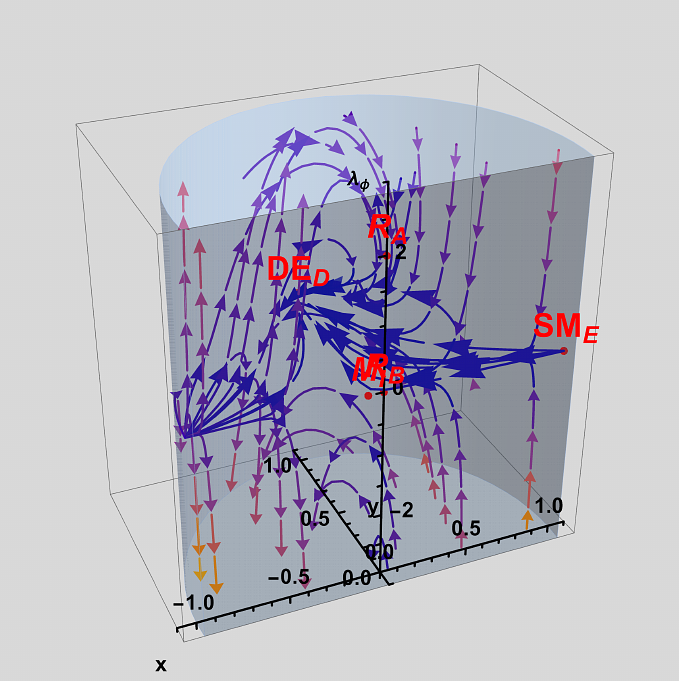
We revisit non-minimally coupled scalar field cosmologies in the Einstein frame and present a comprehensive analysis that spans background dynamics, linear perturbations, thermodynamics, quantum gravity constraints and baryogenesis. Using a dynamical systems approach, we classify all analytical critical points for a representative set of scalar field potentials: axions (ALPs), cyclic ekpyrotic, exponential (ekpyrotic) with $\Lambda$, quintessence, and scalar field dark matter. We show that a chameleon-like coupling $f(\phi)=e^{\beta\phi}$ modifies both the expansion history and the growth of structure in a way that remains compatible with current fifth-force searches. Analytical transfer matrices for primordial tensor modes are derived, revealing a scale-dependent break in the gravitational-wave spectrum whose position and amplitude are fixed by the coupling parameter $\beta$. A causal Israel--Stewart treatment demonstrates that the same coupling supplies an effective bulk pressure that drives a smooth bounce while respecting quantum energy inequalities. Penrose's Weyl-curvature hypothesis is recovered dynamically: during an ekpyrotic phase with $\omega\gg1$ the Weyl invariant decays as $a^{-6(1+\omega)}$, resetting gravitational entropy without violating the generalized second law. A time-varying $\phi$ simultaneously generates an effective chemical potential $\mu_{B}\simeq\beta\dot{\phi}/M^{2}$, allowing for spontaneous high-scale baryogenesis whose back reaction on $\phi$ is negligible for $M\gtrsim10^{15}\sqrt{\beta}$ GeV. Swampland distance and de Sitter criteria are automatically satisfied because the ekpyrotic phase confines the field excursion to $\Delta\phi\lesssim\mathcal{O}(1)M_{\rm Pl}$. These results establish new links between dark-sector interactions, entropy production, and late-time acceleration while identifying observational windows.