Mingyu Kang, Yikang Zhang, Kenneth R. Brown, Thomas Barthel

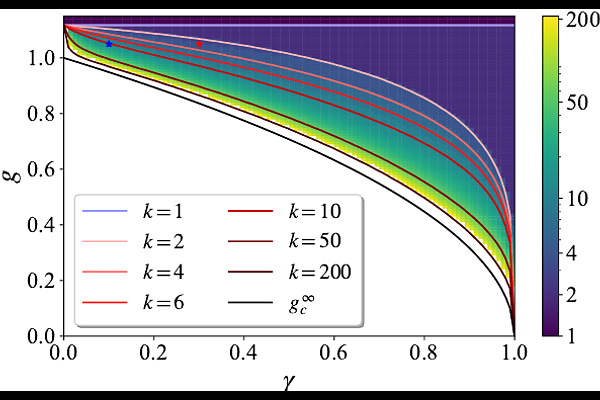
The open quantum Rabi model describes a two-level system coupled to a harmonic oscillator. A Gaussian phase transition for the nonequilibrium steady states has been predicted when the bosonic mode is soft and subject to damping. We show that oscillator dephasing is a relevant perturbation, which leads to a non-Gaussian phase transition and an intriguing cascade of instabilities for $k$-th order bosonic operators. For the soft-mode limit, the equations of motion form a closed hierarchy and spectral properties can be efficiently studied. To this purpose, we establish a fruitful connection to non-Hermitian Hamiltonians. The results for the phase diagram, stability boundaries, and relevant observables are based on mean-field analysis, exact diagonalization, perturbation theory, and Keldysh field theory.