Cavity-induced charge transfer in periodic systems: length-gauge formalism
Voices Powered by
Connected to paperThis paper is a preprint and has not been certified by peer review
Cavity-induced charge transfer in periodic systems: length-gauge formalism
Ekaterina Vlasiuk, Valerii K. Kozin, Jelena Klinovaja, Daniel Loss, Ivan V. Iorsh, Ilya V. Tokatly
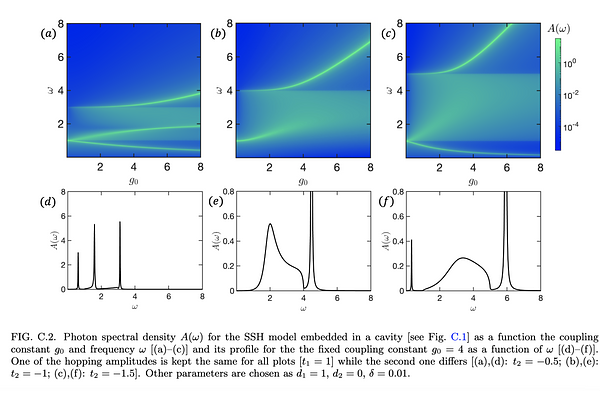
AbstractWe develop a length-gauge formalism for treating one-dimensional periodic lattice systems in the presence of a photon cavity inducing light-matter interaction. The purpose of the formalism is to remove mathematical ambiguities that occur when defining the position operator in the context of the Power-Zienau-Woolley Hamiltonian. We then use a diagrammatic approach to analyze perturbatively the interaction between an electronic quantum system and a photonic cavity mode of long wavelength. We illustrate the versatility of the formalism by studying the cavity-induced electric charge imbalance and polarization in the Rice-Mele model with broken inversion symmetry.
5 comments
scicastboard
Thank you for your contribution. There is a question from an expert in our Scientific Board.
"It is a bit unclear what problem the paper is attempting to solve. There is a standard gauge-matter coupling that is introduced through a co-variant derivative k->k -eA. In the context of solids, A, is a classical (non-fluctuating) field, in the context of standard QED, A is a free fluctuating quantum field, for cavities it's also fluctuating but constrained by a finite-size quantization of the cavity light. It would be helpful if the authors could clarify, why the standard (and in my opinion the only) way to couple to a gauge field is not correct or problematic here?"
Thank you,
ScienceCast scientific board
"It is a bit unclear what problem the paper is attempting to solve. There is a standard gauge-matter coupling that is introduced through a co-variant derivative k->k -eA. In the context of solids, A, is a classical (non-fluctuating) field, in the context of standard QED, A is a free fluctuating quantum field, for cavities it's also fluctuating but constrained by a finite-size quantization of the cavity light. It would be helpful if the authors could clarify, why the standard (and in my opinion the only) way to couple to a gauge field is not correct or problematic here?"
Thank you,
ScienceCast scientific board
kozin-valera
"It would be helpful if the authors could clarify, why the standard (and in my opinion the only) way to couple to a gauge field is not correct or problematic here" -- this not claimed at all. In the paper, the Hamiltonian we start with is obtained via the k->k -eA prescription as it should be. The problem that has been solved, is how to do the diagrammatic calculation in 1D cavity QED when treating the system in the length gauge, which is obtained after the unitary transformation applied to the original Hamiltonian.
I will leave my feedback here. Frankly, I did not understand the point of this service: at the current stage it looks like one takes the abstract from a paper and then it is being fed to GPT-4 with the request to reformulate the abstract. And the "podcast" lasts 30 seconds. Maybe in the future it may become helpful, at this stage I do not see any point.
I will leave my feedback here. Frankly, I did not understand the point of this service: at the current stage it looks like one takes the abstract from a paper and then it is being fed to GPT-4 with the request to reformulate the abstract. And the "podcast" lasts 30 seconds. Maybe in the future it may become helpful, at this stage I do not see any point.
scicastboard
The points are the following:
1. There is overflow of information and most arXiv papers are not read:
https://arxiv.org/stats/monthly_submissions
Short introductory pitches are a useful tool to disseminate information as an entry point into the paper, so that at least it is read (assuming the authors want the paper to be read, which may or may not be the case with this particular preprint).
2. Traditional peer review system is inefficient: referee reports are superficial and often biased. Open peer review puts pressure on both referees and authors to provide hopefully higher-quality content, instead of gambling with submissions to PRL and other venues. It's similar to https://scipost.org/. The ScienceCast peer review system is underdevelopment is coming up within a year.
3. There is a new policy mandating that all US federally funded research be publicly available in accessible format:
https://www.whitehouse.gov/ostp/news-updates/2022/08/25/ostp-issues-guidance-to-make-federally-funded-research-freely-available-without-delay/
So, Dr. Kozin, it's another layer above arXiv to address the three issues: overflow of data, open peer review, and accessibility feature.
Authors not interested in any of this or not comfortable in open discussion of their research are not required to use it. There is a delete button in the right upper corner.
1. There is overflow of information and most arXiv papers are not read:
https://arxiv.org/stats/monthly_submissions
Short introductory pitches are a useful tool to disseminate information as an entry point into the paper, so that at least it is read (assuming the authors want the paper to be read, which may or may not be the case with this particular preprint).
2. Traditional peer review system is inefficient: referee reports are superficial and often biased. Open peer review puts pressure on both referees and authors to provide hopefully higher-quality content, instead of gambling with submissions to PRL and other venues. It's similar to https://scipost.org/. The ScienceCast peer review system is underdevelopment is coming up within a year.
3. There is a new policy mandating that all US federally funded research be publicly available in accessible format:
https://www.whitehouse.gov/ostp/news-updates/2022/08/25/ostp-issues-guidance-to-make-federally-funded-research-freely-available-without-delay/
So, Dr. Kozin, it's another layer above arXiv to address the three issues: overflow of data, open peer review, and accessibility feature.
Authors not interested in any of this or not comfortable in open discussion of their research are not required to use it. There is a delete button in the right upper corner.
kozin-valera
Don't get me wrong, the idea is very cool and I do want to see the features you mentioned of course. My point was that at this stage there is no much difference that I see between what your project does and what would GPT-4 had done have you fed the abstract to it. I'm especially excited about peer-review, that sounds amazing. I will follow ScienceCast and look forward to seeing the futures you mentioned
scicastboard
Actually, the uses are encouraged to upload their own content, see e.g., here:
https://sciencecast.org/casts/oighdx5t4n28
https://sciencecast.org/casts/oighdx5t4n28