Efficiency of neural-network state representations of one-dimensional quantum spin systems

Ruizhi Pan Joint Quantum Institute, NIST/University of Maryland, College Park, MD, USA, Charles W. Clark Joint Quantum Institute, NIST/University of Maryland, College Park, MD, USA National Institute of Standards and Technology, Gaithersburg, Maryland, USA

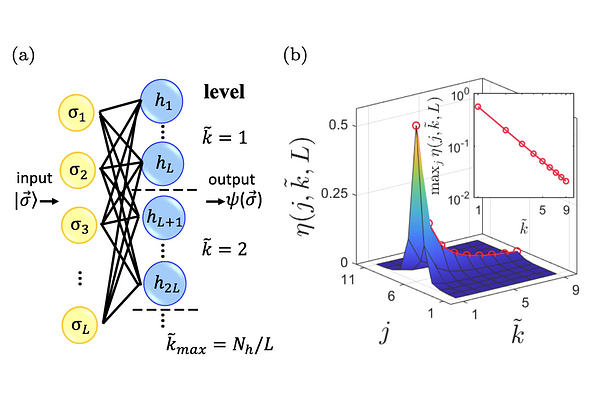
Neural-network state representations of quantum many-body systems are attracting great attention and more rigorous quantitative analysis about their expressibility and complexity is warranted. Our analysis of the restricted Boltzmann machine (RBM) state representation of one-dimensional (1D) quantum spin systems provides new insight into their computational complexity. We define a class of long-range-fast-decay (LRFD) RBM states with quantifiable upper bounds on truncation errors and provide numerical evidence for a large class of 1D quantum systems that may be approximated by LRFD RBMs of at most polynomial complexities. These results lead us to conjecture that the ground states of a wide range of quantum systems may be exactly represented by LRFD RBMs or a variant of them, even in cases where other state representations become less efficient. At last, we provide the relations between multiple typical state manifolds. Our work proposes a paradigm for doing complexity analysis for generic long-range RBMs which naturally yields a further classification of this manifold. This paradigm and our characterization of their nonlocal structures may pave the way for understanding the natural measure of complexity for quantum many-body states described by RBMs and are generalizable for higher-dimensional systems and deep neural-network quantum states.