P. V. Sriluckshmy, François Jamet, Fedor Šimkovic IV

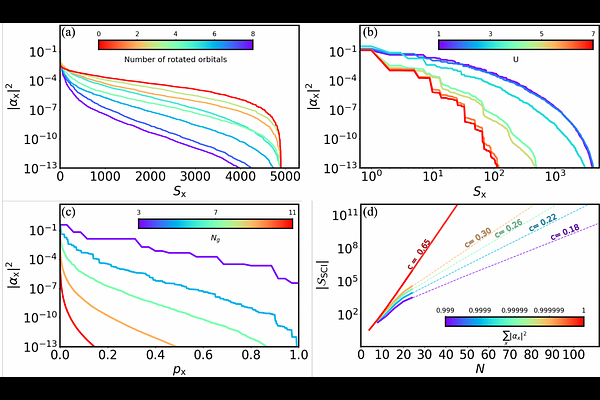
The ghost Gutzwiller ansatz (gGut) embedding technique was shown to achieve comparable accuracy to the gold standard dynamical mean-field theory method in simulating real material properties, yet at a much lower computational cost. Despite that, gGut is limited by the algorithmic bottleneck of computing the density matrix of the underlying effective embedding model, a quantity which must be converged within a self-consistent embedding loop. We develop a hybrid quantum-classical gGut technique which computes the ground state properties of embedding Hamiltonians with the help of a quantum computer, using the sample-based quantum-selected configuration interaction (QSCI) algorithm. We study the applicability of SCI-based methods to the evaluation of the density of states for single-band Anderson impurity models within gGut and find that such ground states of interest become sufficiently sparse in the CI basis as the number of ghost orbitals is increased. Further, we investigate the performance of QSCI using local unitary cluster Jastrow (LUCJ) variational quantum states in combination with a circuit cutting technique, prepared on IQM's quantum hardware for system sizes of up to 11 ghost orbitals, equivalent to 24 qubits. We report converged gGut calculations which correctly capture the metal-to-insulator phase transition in the Fermi-Hubbard model on the Bethe lattice by using quantum samples to build an SCI basis with as little as $1\%$ of the total CI basis states.