Verena Brehm, Olena Gomonay, Serban Lepadatu, Mathias Kläui, Jairo Sinova, Arne Brataas, Alireza Qaiumzadeh

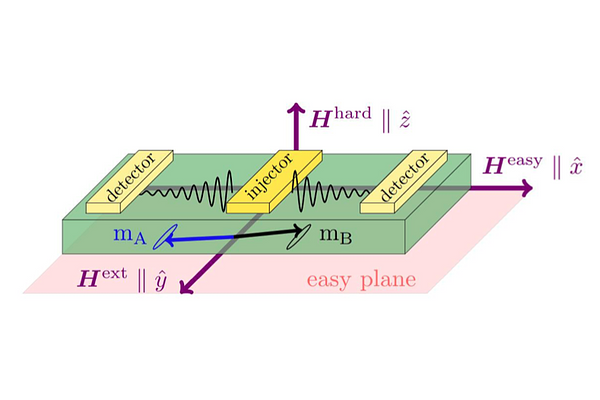
Magnon eigenmodes in easy-plane antiferromagnetic insulators are linearly polarized and are not expected to carry any net spin angular momentum. Motivated by recent nonlocal spin transport experiments in the easy-plane phase of hematite, we perform a series of micromagnetic simulations in a nonlocal geometry at finite temperatures. We show that by tuning an external magnetic field, we can control the magnon eigenmodes and the polarization of the spin transport signal in these systems. We argue that a coherent beating oscillation between two orthogonal linearly polarized magnon eigenmodes is the mechanism responsible for finite spin transport in easy-plane antiferromagnetic insulators. The sign of the detected spin signal is also naturally explained by the proposed coherent beating mechanism. Our finding opens a path for on-demand control of the spin signal in a large class of easy-plane antiferromagnetic insulators.