Bharath Hebbe Madhusudhana

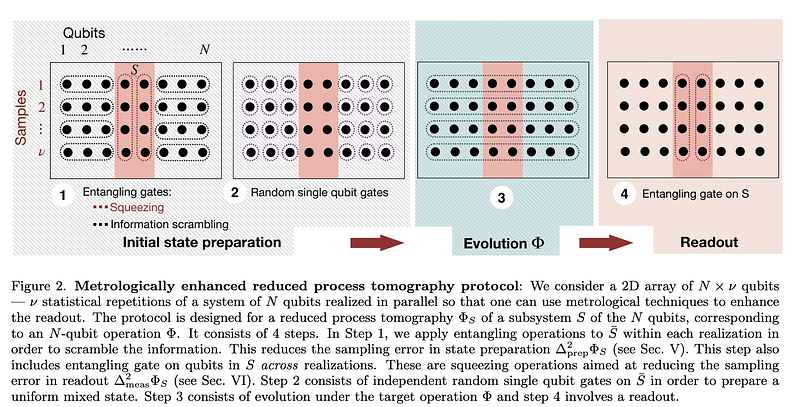
Accurate and precise control of large quantum systems is paramount to achieve practical advantages on quantum devices. Therefore, benchmarking the hardware errors in quantum computers has drawn significant attention lately. Existing benchmarks for digital quantum computers involve averaging the global fidelity over a large set of quantum circuits and are therefore unsuitable for specific multi-qubit gates used in analog quantum operations. Moreover, average global fidelity is not the optimal figure-of-merit for some of the applications specific to multi-qubit gates and analog devices , such as the study of many-body physics, which often use local observables. In this two-part paper, we develop a new figure-of-merit suitable for multi-qubit quantum gates based on the reduced Choi matrix of the operation. In the first part, we develop an efficient, scalable protocol to completely characterize the reduced Choi matrix. We identify two sources of sampling errors in measurements of the reduced Choi matrix and we show that there are fundamental limits to the rate of convergence of the sampling errors, analogous to the standard quantum limit and Heisenberg limit. A slow convergence rate of sampling errors would mean that we need a large number of experimental shots. We develop protocols using quantum information scrambling, which has been observed in disordered systems for e.g., to speed up the rate of convergence of the sampling error at state preparation Moreover, we develop protocols using squeezed and entangled initial states to enhance the convergence rate of the sampling error at measurement, which results in a metrologically enhanced reduced process tomography protocol.