Fedor K. Popov, Grigory Tarnopolsky

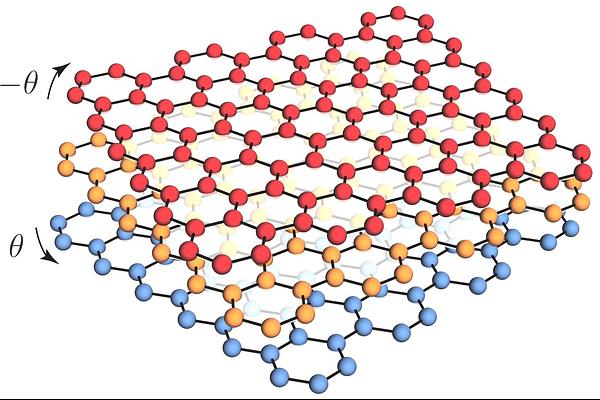
We consider a configuration of three stacked graphene monolayers with equal consecutive twist angles $\theta$. Remarkably, in the chiral limit when interlayer coupling terms between $\textrm{AA}$ sites of the moir\'{e} pattern are neglected we find four perfectly flat bands (for each valley) at a sequence of magic angles which are exactly equal to the twisted bilayer graphene (TBG) magic angles divided by $\sqrt{2}$. Therefore, the first magic angle for equal-twist trilayer graphene (eTTG) in the chiral limit is $\theta_{*} \approx 1.05^{\circ}/\sqrt{2} \approx 0.74^{\circ}$. We prove this relation analytically and show that the Bloch states of the eTTG's flat bands are non-linearly related to those of TBG's. Additionally, we show that at the magic angles, the upper and lower bands must touch the four exactly flat bands at the Dirac point of the middle graphene layer. Finally, we explore the eTTG's spectrum away from the chiral limit through numerical analysis.