Andreas Sinner, Pierre A. Pantaleón, Francisco Guinea

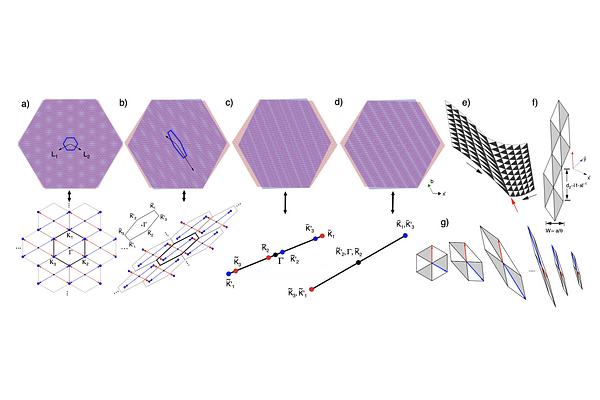
We study the effects of strain in moir\'e systems composed of honeycomb lattices. We elucidate the formation of almost perfect one-dimensional moir\'e patterns in twisted bilayer systems. The formation of such patterns is a consequence of an interplay between twist and strain which gives rise to a collapse of the reciprocal space unit cell. As a criterion for such collapse we find a simple relation between the two quantities and the material specific Poisson ratio. The induced one dimensional behavior is characterized by two, usually incommensurate, periodicities. Our results offer explanations for the complex patterns of one-dimensional channels observed in low angle twisted bilayer graphene systems and twisted bilayer dicalcogenides. Our findings can be applied to any hexagonal twisted moir\'e pattern and can be easily extended to other geometries.