Gabriel A. Durkin

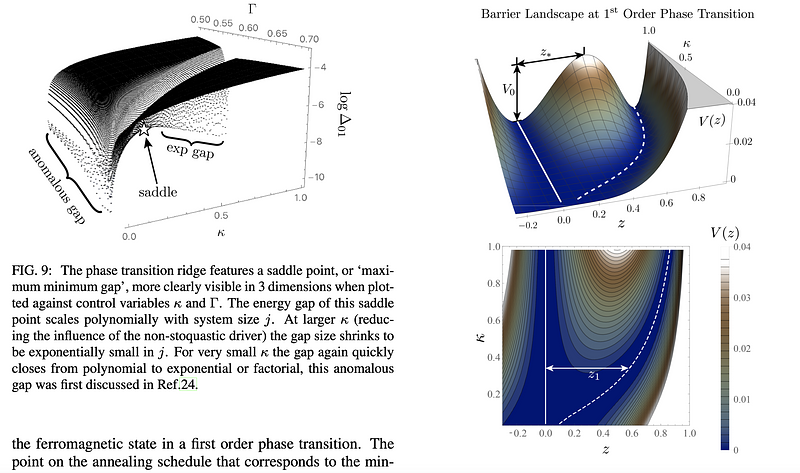
It is known that secondary non-stoquastic drivers may offer speed-ups or catalysis in some models of adiabatic quantum computation accompanying the more typical transverse field driver. Their combined intent is to raze potential barriers to zero during adiabatic evolution from a false vacuum to a true minimum; first order phase transitions are softened into second order transitions. We move beyond mean-field analysis to a fully quantum model of a spin ensemble undergoing adiabatic evolution in which the spins are mapped to a variable mass particle in a continuous one-dimensional potential. We demonstrate the necessary criteria for enhanced mobility or `speed-up' across potential barriers is actually a quantum form of the Rayleigh criterion. Quantum catalysis is exhibited in models where previously thought not possible, when barriers cannot be eliminated. For the $3$-spin model with secondary anti-ferromagnetic driver, catalysed time complexity scales between linear and quadratically with the number of qubits. As a corollary, we identify a useful resonance criterion for quantum phase transition that differs from the classical one, but converges on it, in the thermodynamic limit.