Sergey Bravyi, Robert Manson-Sawko, Mykhaylo Zayats, Sergiy Zhuk

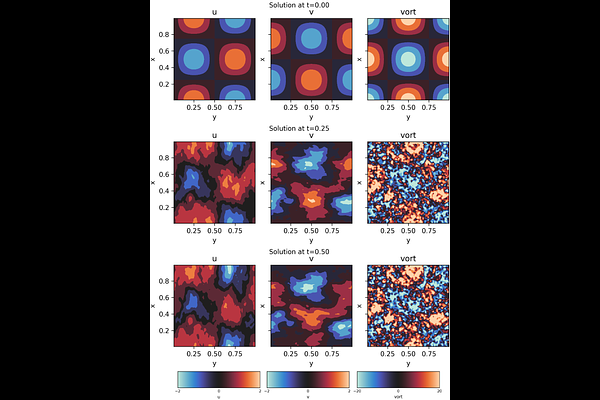
We consider the problem of simulating dynamics of classical nonlinear dissipative systems with $N\gg 1$ degrees of freedom. To make the problem tractable for quantum computers, we add a weak Gaussian noise to the equation of motion and the initial state. Our main result is an end-to-end quantum algorithm for simulating the noisy dynamics of nonlinear systems satisfying certain sparsity and divergence-free conditions. For any constant nonzero noise rate, the quantum runtime scales polynomially with $\log{(N)}$, evolution time, inverse error tolerance, and the relative strength of nonlinearity and dissipation. Our main technical tool is the Kolmogorov partial differential equation describing time evolution of scalar functions of solutions, averaged over noise. To enable efficient quantum simulation, we project the Kolmogorov equation onto the space of low degree polynomials and derive a rigorous upper bound on the resulting approximation error, which may be of independent interest. Finally, we show that the considered simulation problem is BQP-complete, meaning that it is as hard as simulating the universal quantum computer. We demonstrate the efficacy of our algorithm by simulating it numerically for two paradigmatic nonlinear systems: an anharmonic oscillator and the 2D Navier Stokes equation.