Bharath Hebbe Madhusudhana

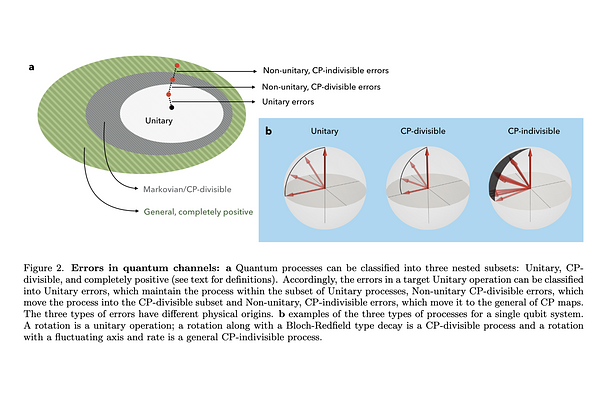
An important step in developing multi-qubit gates is to construct efficient benchmarking protocols for them. In our previous paper (arXiv: 2210.04330), we developed metrological protocols to measure the reduced Choi matrix i.e., the completely positive (CP) maps induced on a subset S of the qubits, by the multi-qubit gate. Here, we show a set of classically verifiable properties that the Choi matrix satisfies if it is a reduction of a multi-qubit unitary and use them to develop benchmarks. We identify three types of errors that affect the implementation of a multi-qubit unitary, based on their mathematical properties and physical origin. Although a target multi-qubit gate is a unitary operator, errors turn it into a general completely positive (CP) map. Errors due to coupling to a thermal bath result in the multi-qubit gate being CP-divisible (Markovian), deviating from a unitary. The reduced Choi matrix of a multi-qubit gate has a property known as double stochasticity, which is violated in the presence of Markovian errors. We construct a benchmark using double-stochasticity violation and show that it is sensitive to coupling to any thermal bath at a finite temperature. Further, errors due to shot-to-shot fluctuations result in a non-markovian, i.e., CP-indivisible quantum process. We prove a new property, which we call the \rank property of the reduced Choi matrix, the violation of which implies a CP-indivisible error. A third category of errors comes from systematics in the implementation of a multi-qubit gate, resulting in no deviation from unitarity. We refer to this as unitary errors. This corresponds to the most challenging type of error to benchmark. We develop a partial-benchmarking protocol for such errors using symmetries of the multi-qubit gate being applied.