Deep quantum neural networks form Gaussian processes

Diego García-Martín, Martin Larocca, M. Cerezo

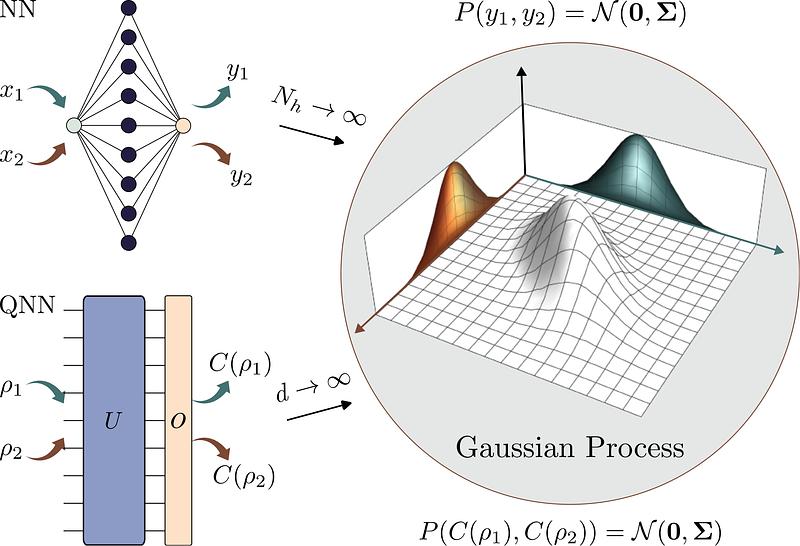
It is well known that artificial neural networks initialized from independent and identically distributed priors converge to Gaussian processes in the limit of large number of neurons per hidden layer. In this work we prove an analogous result for Quantum Neural Networks (QNNs). Namely, we show that the outputs of certain models based on Haar random unitary or orthogonal deep QNNs converge to Gaussian processes in the limit of large Hilbert space dimension $d$. The derivation of this result is more nuanced than in the classical case due the role played by the input states, the measurement observable, and the fact that the entries of unitary matrices are not independent. An important consequence of our analysis is that the ensuing Gaussian processes cannot be used to efficiently predict the outputs of the QNN via Bayesian statistics. Furthermore, our theorems imply that the concentration of measure phenomenon in Haar random QNNs is much worse than previously thought, as we prove that expectation values and gradients concentrate as $\mathcal{O}\left(\frac{1}{e^d \sqrt{d}}\right)$ -- exponentially in the Hilbert space dimension. Finally, we discuss how our results improve our understanding of concentration in $t$-designs.