Tathagata Ghosh, Sukanta Bose, Sanjeev Dhurandhar, Sunil Choudhary

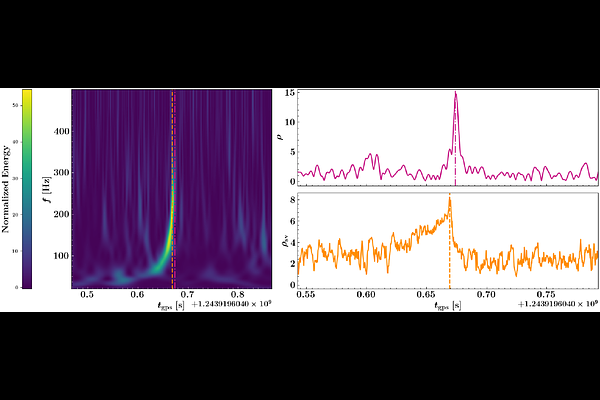
The sensitivity of current gravitational wave (GW) detectors to transient GW signals is severely affected by a variety of non-Gaussian and non-stationary noise transients, such as the blip and tomte "glitches". These glitches share some time-frequency resemblance with GW signals from massive binary black holes. In earlier works [Joshi et al., Phys. Rev. D 103, 044035 (2021); Choudhary et al., Phys. Rev. D 110, 044051 (2024)], the authors presented a method for constructing a $\chi^2$-distributed optimized statistic, based on the unified formalism of $\chi^2$ discriminators [Dhurandhar et al., Phys. Rev. D 96, 103018 (2017)], to distinguish the blip and tomte glitches from the compact binary coalescence (CBC) signals. Unlike past works, the new $\chi^2$ discriminator is constructed from the most significant singular vectors obtained from the singular-value decomposition (SVD) of glitches in real detector data. We find that the chi-square developed in this work performs as efficiently as in Choudhary et al. [Phys. Rev. D 110, 044051 (2024)], which used sine-Gaussian basis vectors. This result supports past empirical findings that the blips and tomtes are well-modeled by sine-Gaussians. It also introduces a method for constructing signal- and glitch-based $\chi^2$ discriminators by directly using real data containing the glitches and, thus, holds promise for extensions to glitches that are captured less well by sine-Gaussians or other analytical functions.