Regular Power-Maxwell Black Holes
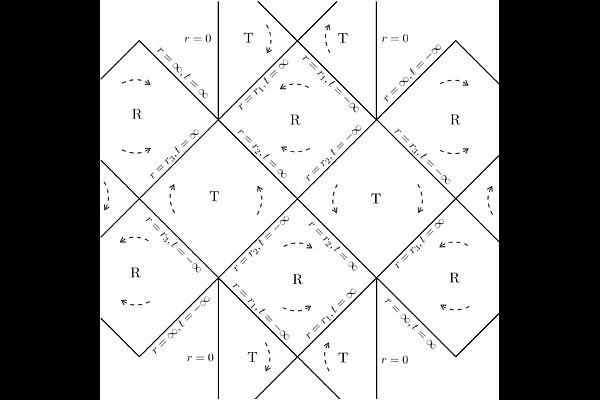
Regular Power-Maxwell Black Holes
Yi-bo Liang, Hong-Rong Li
AbstractWe present a new class of regular, spherically symmetric spacetimes in nonlinear electrodynamics that are asymptotically dynamical but not de Sitter, exhibiting power-law Maxwell behavior at infinity. Starting from magnetic solutions, we demonstrate that the weak energy condition is satisfied, while the dominant energy condition is also fulfilled. These configurations are extended to include regular black holes, with their existence conditions and global structures analyzed via novel Penrose diagrams. Through FP duality, we obtain corresponding electric solutions and establish uniqueness criteria. However, in square-root--Maxwell theory, electric duals are absent; we address this by introducing an auxiliary scalar field formulation that restores duality and yields a generalized transformation. We further investigate the effective metric governing light propagation, finding that it remains regular for some magnetic cases (in the absence of black holes) but becomes singular for electric ones. Furthermore, we identify spacelike photon trajectories in these spacetimes, signaling the existence of causality issues. Finally, we derive the first law and Smarr formula, showing the existence of thermodynamically stable black holes with positive heat capacity.