Junpei Harada

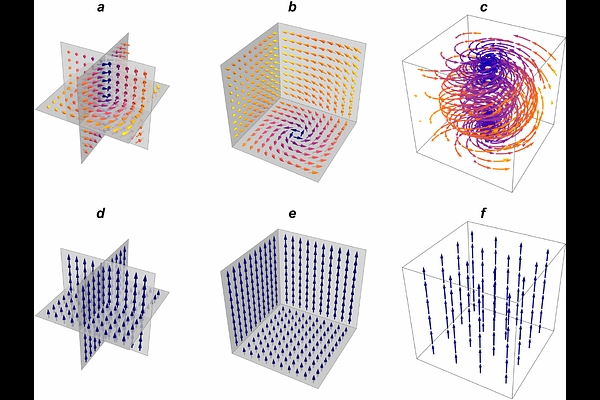
An exact solution to the vacuum Einstein equations is presented, whose structure is based on the Hopf fibration. The solution employs a geodesic null vector field that defines a twisting congruence and appears in the metric in Kerr-Schild form. This solution is of Petrov type D and involves two parameters. Remarkably, the resulting spacetime is regular, with no curvature singularities. Both the Kretschmann scalar and the Chern-Pontryagin scalar are nonzero and remain finite throughout the spacetime. In addition, the Newman-Penrose Weyl scalar $\Psi_2$ possesses both nonzero real and imaginary parts, reflecting the topologically nontrivial nature of the gravitational field. The spacetime also admits two Killing vector fields and a Killing-Yano tensor, which induces an associated Killing tensor, revealing its hidden symmetry. The derivation is simple and self-contained, offering a transparent and geometrically guided approach to finding new exact solutions in general relativity.