Quantum spherical codes
Voice is AI-generated
Connected to paperThis paper is a preprint and has not been certified by peer review
Quantum spherical codes
Shubham P. Jain, Joseph T. Iosue, Alexander Barg, Victor V. Albert
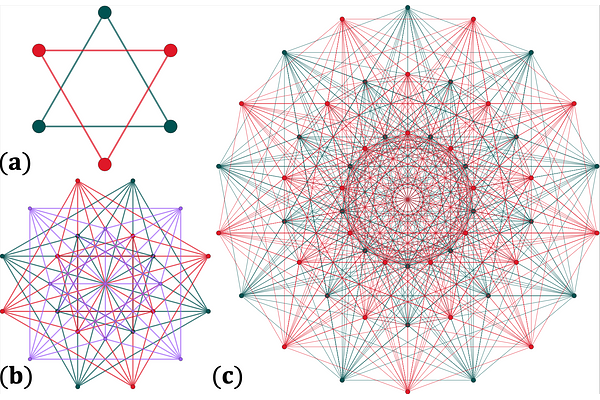
AbstractWe introduce a framework for constructing quantum codes defined on spheres by recasting such codes as quantum analogues of the classical spherical codes. We apply this framework to bosonic coding, obtaining multimode extensions of the cat codes that can outperform previous constructions while requiring a similar type of overhead. Our polytope-based cat codes consist of sets of points with large separation that at the same time form averaging sets known as spherical designs. We also recast concatenations of qubit CSS codes with cat codes as quantum spherical codes.
2 comments
scicastboard
Dr. Albert -- Thank you for posting a summary of your exciting and potentially impactful paper.
Classical spherical codes are useful in protecting classical information from noise, do you show or suggest that similarly quantum codes have an intrinsic error correction built in?
Also, purely visually, your pictorial representation of the codes resembles that of classification of Lie algebras. Is it just a visual similarity or there is a potentially deeper connection?
For important papers like this, we recommend posting "human" summary of results as AI-summaries have their limitations in explaining the complexity of the the work.
ScienceCast CS/QI moderators
Classical spherical codes are useful in protecting classical information from noise, do you show or suggest that similarly quantum codes have an intrinsic error correction built in?
Also, purely visually, your pictorial representation of the codes resembles that of classification of Lie algebras. Is it just a visual similarity or there is a potentially deeper connection?
For important papers like this, we recommend posting "human" summary of results as AI-summaries have their limitations in explaining the complexity of the the work.
ScienceCast CS/QI moderators
valbert4
Thanks for the questions!
Re quantum codes: Yes, these quantum codes are inspired from the classical spherical codes with the aim of protecting against noise in quantum systems. We do show that these codes protect against certain kinds of errors that are prominent for our setting of coherent states, namely excitation losses, gains and angular dephasing.
Re Lie algebras: Great question! There is a deeper connection here which we do not talk about in the manuscript since it’s not particularly useful for our purposes. Our code states are superpositions of vertices of regular polytopes. Many of these polytopes are spanned by the root vector system of simple Lie algebras. For example: the Witting polytope is a lattice shell of the E_8 lattice and is spanned by the root system (in R^8) of the exceptional simple Lie algebra E8. Many of these polytopes also relate to the minuscule representations of simple Lie algebras elaborated in arXiv:0704.2254 for example. Polytopes coming from these exceptional Lie algebras have produced quite good codes and provide motivation to search further for similar structures.
Re quantum codes: Yes, these quantum codes are inspired from the classical spherical codes with the aim of protecting against noise in quantum systems. We do show that these codes protect against certain kinds of errors that are prominent for our setting of coherent states, namely excitation losses, gains and angular dephasing.
Re Lie algebras: Great question! There is a deeper connection here which we do not talk about in the manuscript since it’s not particularly useful for our purposes. Our code states are superpositions of vertices of regular polytopes. Many of these polytopes are spanned by the root vector system of simple Lie algebras. For example: the Witting polytope is a lattice shell of the E_8 lattice and is spanned by the root system (in R^8) of the exceptional simple Lie algebra E8. Many of these polytopes also relate to the minuscule representations of simple Lie algebras elaborated in arXiv:0704.2254 for example. Polytopes coming from these exceptional Lie algebras have produced quite good codes and provide motivation to search further for similar structures.