Po-Chieh Liu, Christoph Hirche, Hao-Chung Cheng

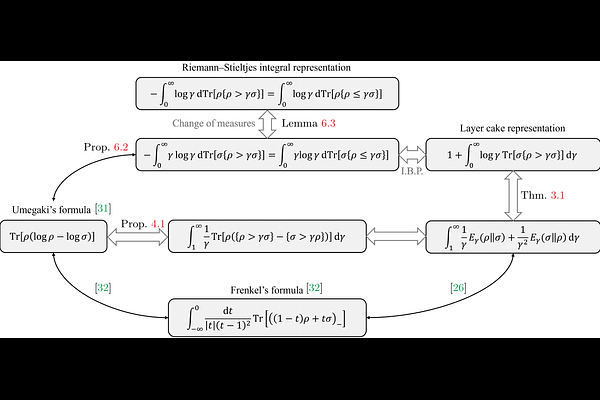
Defining suitable quantum extensions of classical divergences often poses a challenge due to the non-commutative nature of quantum information. In this work, we propose a new approach via what we call the layer cake representation. The resulting quantum R\'enyi and $f$-divergences are then proven to be equivalent to those recently defined via integral representations. Nevertheless, the approach can provide several insights. We give an alternative proof of the integral representation of the relative entropy by Frenkel and prove a conjecture regarding a trace expression for the R\'enyi divergence. Additionally, we give applications to error exponents in hypothesis testing, a new Riemann-Stieltjes type integral representation and a variational representation.