Yi Zhou, Rodrigo Panosso Macedo

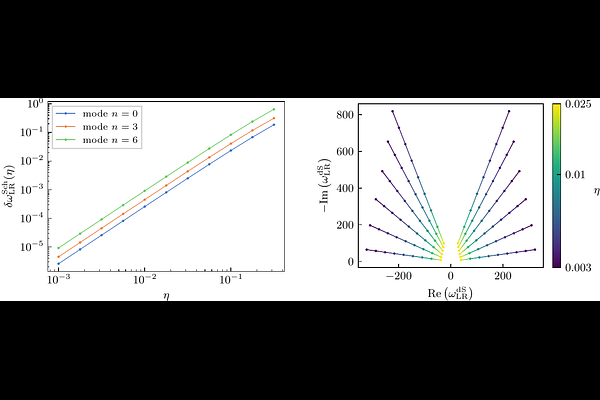
We revisit the quasinormal mode problem in Schwarzschild--de Sitter spacetimes providing a unified infrastructure tailored for studying limiting configurations. Geometrically, we employ the hyperboloidal framework to explicitly implement Geroch's rigorous limiting procedures for families of spacetimes. This enables a controlled transition between Schwarzschild, de Sitter, and Nariai geometries. Numerically, we introduce the analytical mesh refinement technique into quasinormal mode calculations, successfully recovering -- within the appropriate limiting scenarios -- both known families of quasinormal modes: complex light-ring modes and purely imaginary de Sitter modes. We interpret these results in terms of spectral instability, where the notions of stable and unstable modes depends on the specific spacetime limit under consideration. In the Schwarzschild limit, de Sitter modes appear as a destabilizing effect on the continuous branch cut at $\omega = 0$. Conversely, the branch cut can be understood as emerging from an infinite accumulation of discrete modes at $\omega = 0$ in the transitional regime. We propose a heuristic measure of QNM density to characterize this accumulation and highlight the need for a more rigorous study of potential branch cut instabilities--especially relevant in the context of late-time gravitational wave signals. The proposed infrastructure provides a general and extensible framework for investigations in more complex spacetimes, such as Reissner--Nordstr\"om--de Sitter or Kerr--Newman--de Sitter.