Bharath Hebbe Madhusudhana, Sebastian Scherg, Thomas Kohlert, Immanuel Bloch, Monika Aidelsburger

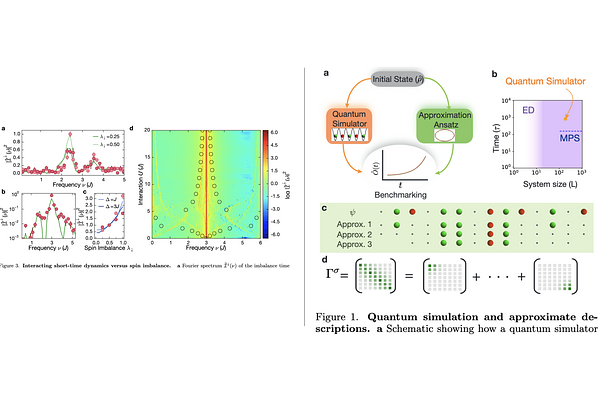
Quantum simulators have made a remarkable progress towards exploring the dynamics of many-body systems, many of which offer a formidable challenge to both theoretical and numerical methods. While state-of-the-art quantum simulators are in principle able to simulate quantum dynamics well outside the domain of classical computers, they are noisy and limited in the variability of the initial state of the dynamics and the observables that can be measured. Despite these limitations, here we show that such a quantum simulator can be used to in-effect solve for the dynamics of a many-body system. We develop an efficient numerical technique that facilitates classical simulations in regimes not accessible to exact calculations or other established numerical techniques. The method is based on approximations that are well suited to describe localized one-dimensional Fermi-Hubbard systems. Since this new method does not have an error estimate and the approximations do not hold in general, we use a neutral-atom Fermi-Hubbard quantum simulator with $L_{\text{exp}}\simeq290$ lattice sites to benchmark its performance in terms of accuracy and convergence for evolution times up to $700$ tunnelling times. We then use these approximations in order to derive a simple prediction of the behaviour of interacting Bloch oscillations for spin-imbalanced Fermi-Hubbard systems, which we show to be in quantitative agreement with experimental results. Finally, we demonstrate that the convergence of our method is the slowest when the entanglement depth developed in the many-body system we consider is neither too small nor too large. This represents a promising regime for near-term applications of quantum simulators.