Jonas El Gammal, Riccardo Buscicchio, Germano Nardini, Jesús Torrado

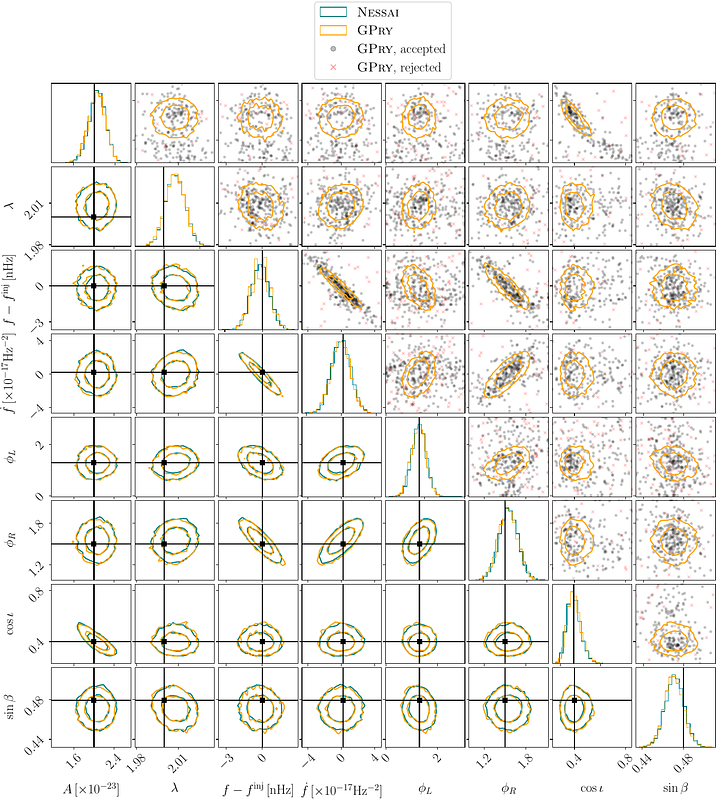
Source inference for deterministic gravitational waves is a computationally demanding task in LISA. In a novel approach, we investigate the capability of Gaussian Processes to learn the posterior surface in order to reconstruct individual signal posteriors. We use GPry, which automates this reconstruction through active learning, using a very small number of likelihood evaluations, without the need for pretraining. We benchmark GPry against the cutting-edge nested sampler nessai, by injecting individually three signals on LISA noisy data simulated with Balrog: a white dwarf binary (DWD), a stellar-mass black hole binary (stBHB), and a super-massive black hole binary (SMBHB). We find that GPry needs $\mathcal O(10^{-2})$ fewer likelihood evaluations to achieve an inference accuracy comparable to nessai, with Jensen-Shannon divergence $D_{\scriptscriptstyle \mathrm{JS}} \lesssim 0.01$ for the DWD, and $D_{\scriptscriptstyle \mathrm{JS}} \lesssim 0.05$ for the SMBHB. Lower accuracy is found for the less Gaussian posterior of the stBHB: $D_{\scriptscriptstyle \mathrm{JS}} \lesssim 0.2$. Despite the overhead costs of GPry, we obtain a speed-up of $\mathcal O(10^2)$ for the slowest cases of stBHB and SMBHB. In conclusion, active-learning Gaussian process frameworks show great potential for rapid LISA parameter inference, especially for costly likelihoods, enabling suppression of computational costs without the trade-off of approximations in the calculations.