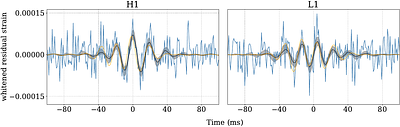
Gravitational-wave astronomy provides a promising avenue for the discovery of new physics beyond general relativity as it probes extreme curvature and ultra-relativistic dynamics. However, in the absence of a compelling alternative to general relativity, it is difficult to carry out an analysis that allows for a wide range of deviations. To that end, we introduce a Gaussian process framework to search for deviations from general relativity in gravitational-wave signals from binary black hole mergers with minimal assumptions. We employ a kernel that enforces our prior beliefs that - if gravitational waveforms deviate from the predictions of general relativity - the deviation is likely to be localised in time near the merger with some characteristic frequency. We demonstrate this formalism with simulated data and apply it to events from Gravitational-Wave Transient Catalog 3. We find no evidence for a deviation from general relativity. We limit the fractional deviation in gravitational-wave strain to as low as 7% (90% credibility) of the strain of GW190701_203306. less

We show that the random adjacency matrices induced by the chronological relations and i.i.d. samples of two spacetimes coincide in law if and only if the spacetimes in question are smoothly isometric. A similar result holds for weighted spacetimes. In the smooth framework of our article, this relaxes the hypotheses of the recent Gromov reconstruction theorem in Lorentzian signature by Braun-S\"amann from a.s. isometry of the respective time separation functions to a.s. order isometry. In a probabilistic way, our result makes a key paradigm of causal set theory rigorous: spacetime can be recovered by only knowing "order" and "number" of its points. It confirms a weak version of Bombelli's conjecture; therefore, it contributes to recent efforts of formalizing the Hauptvermutung (viz. fundamental conjecture) of causal set theory. less

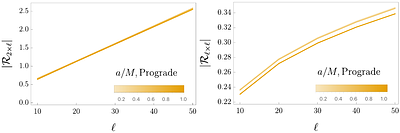
We provide a fully analytical approach to calculate the nonlinearities of the gravitational waves in the ringdown of a Kerr black hole in the eikonal limit. The corresponding quasi-normal modes are associated to the orbits of a closed circular null geodesic and the problem can be analyzed by taking the Penrose limit around it. We calculate analytically the amplitude and the phase of the quadratic quasi-normal modes as well as its dependence on the black hole spin. less

We analyse a stationary, cylindrically symmetric spacetime endowed with an intrinsic helical twist, $ds^{2} = -dt^{2} + dr^{2} + r^{2} d\phi^{2} + (dz + \omega\, r\,d\phi)^{2}$. Solving the Einstein equations exactly yields an anisotropic energy-momentum tensor whose density is negative and decays as $r^{-2}$, thus violating the weak energy condition near the axis. Three notable features emerge: (i) axis-centred negative energy; (ii) unequal transverse stresses; (iii) a torsional momentum flux $T_{\phi z}\omega^{3}/r$. We identify stable photon orbits and deflection angle, fully helical geodesics, and torsion-controlled wave optics modes, suggesting laboratory analogues in twisted liquid-crystal and photonic systems. The coupling between the torsion parameter $\omega$ and other physical parameters leads to significant effects, altering the motion along the positive or negative $z$-axis. These results make the twisted helical metric a useful test bed for studying the interplay of curvature, torsion, and matter in both gravitational and condensed-matter contexts. less

We analyze the thermal fluctuations of a free, conformally invariant, Maxwell quantum field (photon) interacting with a cosmological background spacetime, in the framework of quantum field theory in curved spacetimes and semiclassical and stochastic gravity. The thermal fluctuations give rise to backreaction effects upon the spacetime geometry, which are incorporated in the semiclassical Einstein-Langevin equation, evaluated in the cosmological Friedmann-Lema\^{i}tre-Robertson-Walker spacetime. We first evaluate the semiclassical Einstein equation for the background geometry sourced by the thermal quantum stress-energy tensor. For large enough temperature, the solution is approximated by a radiation-dominated expanding universe driven by the thermal bath of photons. We then evaluate the thermal noise kernel associated to the quantum fluctuations of the photon field using point-splitting regularization methods, and give its explicit analytic form in the limits of large and small temperature, as well as a local approximation. Finally, we prove that this thermal noise kernel corresponds exactly to the thermal variance of the induced fluctuations of the linearized metric perturbation in the local and covariant measurement scheme defined by Fewster and Verch. Our analysis allows to quantify the extent to which quantum fluctuations may give rise to non-classical effects, and thus become relevant in inflationary cosmology. less