Marvin Schmitt, Daniel Habermann, Paul-Christian Bürkner, Ullrich Köthe, Stefan T. Radev

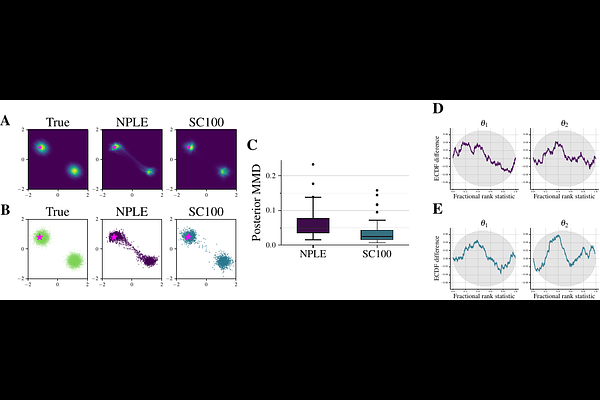
We propose a method to improve the efficiency and accuracy of amortized Bayesian inference (ABI) by leveraging universal symmetries in the probabilistic joint model $p(\theta, y)$ of parameters $\theta$ and data $y$. In a nutshell, we invert Bayes' theorem and estimate the marginal likelihood based on approximate representations of the joint model. Upon perfect approximation, the marginal likelihood is constant across all parameter values by definition. However, approximation error leads to undesirable variance in the marginal likelihood estimates across different parameter values. We formulate violations of this symmetry as a loss function to accelerate the learning dynamics of conditional neural density estimators. We apply our method to a bimodal toy problem with an explicit likelihood (likelihood-based) and a realistic model with an implicit likelihood (simulation-based).