Yun Wang, Jia Ren, Lu-Yao Jiang, Hao Zhou, Yi-Han Iris Yin, Yi-Fang Liang, Zhi-Ping Jin, Yi-Zhong Fan, Da-Ming Wei, Wei Chen, Hui Sun, Jing-Wei Hu, Dong-Yue Li, Jun Yang, Wen-Da Zhang, Yuan Liu, Wei-Min Yuan, Xue-Feng Wu

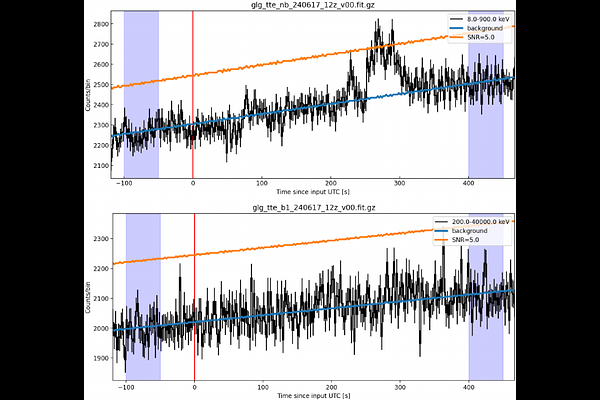
We have developed a lightweight tool {\tt RapidGBM}, featured by a web-based interface and capabilities of rapid calculation of Fermi-GBM visibilities and performing basic data analysis. It has two key features: (1) immediately check the visibility of Fermi-GBM for new transients, and (2) check the light curve and perform spectral analysis after the hourly TTE data is released. The visibility check and the response matrix generation required for spectral analysis can be achieved through the historical pointing file after the orbit calculation, even when the real-time pointing file is not yet available. As a case, we apply the tool to EP240617a, an X-ray transient triggered by Einstein Probe (EP). We demonstrate the workflow of visibility checking, data processing, and spectral analysis for this event. The results suggest that EP240617a can be classified as an X-ray-rich GRB (XRR) and confirm the feasibility of using historical pointing files for rapid analysis. Further, we discuss possible physical interpretations of such events, including implications for jet launching and progenitor scenarios. Therefore, {\tt RapidGBM} is expected to assist Einstein Probe Transient Advocates (EP-TAs), Space-based multi-band astronomical Variable Objects Monitor Burst Advocates (SVOM-BAs), and other members of the community in cross-checking high-energy transients. Based on prompt emission parameter relations (e.g. $E_{\rm p}$-$E_{\gamma,\rm iso}$), it can also help identify peculiar GRBs (e.g. long-short burst, magnetar giant flare, etc.) and and provide useful references (e.g. more accurate $T_0$) for scheduling follow-up observations.