Dean Eckles, Elchanan Mossel, M. Amin Rahimian, Subhabrata Sen

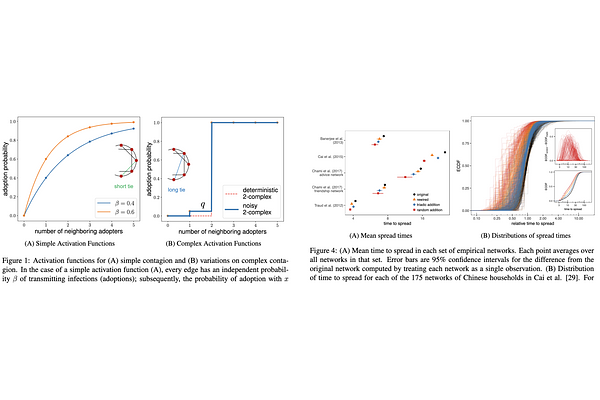
Network structure can affect when and how widely new ideas, products, and behaviors are adopted. In widely-used models of biological contagion, interventions that randomly rewire edges (on average making them "longer") accelerate spread. However, there are other models relevant to social contagion, such as those motivated by myopic best-response in games with strategic complements, in which an individual's behavior is described by a threshold number of adopting neighbors above which adoption occurs (i.e., complex contagions). Recent work has argued that highly clustered, rather than random, networks facilitate spread of these complex contagions. Here we show that minor modifications to this model, which make it more realistic, reverse this result, thereby harmonizing qualitative facts about how network structure affects contagion. To model the trade-off between long and short edges we analyze the rate of spread over networks that are the union of circular lattices and random graphs on $n$ nodes. Allowing for noise in adoption decisions (i.e., adoptions below threshold) to occur with order ${n}^{-1/\theta}$ probability along at least some "short" cycle edges is enough to ensure that random rewiring accelerates the spread of a noisy threshold-$\theta$ contagion. This conclusion also holds under partial but frequent enough rewiring and when adoption decisions are reversible but infrequently so, as well as in high-dimensional lattice structures that facilitate faster-expanding contagions. Simulations illustrate the robustness of these results to several variations on this noisy best-response behavior. Hypothetical interventions that randomly rewire existing edges or add random edges (versus adding "short", triad-closing edges) in hundreds of empirical social networks reduce time to spread.