Learning Minimalistic Tsetlin Machine Clauses with Markov Boundary-Guided Pruning
Learning Minimalistic Tsetlin Machine Clauses with Markov Boundary-Guided Pruning
Ole-Christoffer Granmo, Per-Arne Andersen, Lei Jiao, Xuan Zhang, Christian Blakely, Tor Tveit
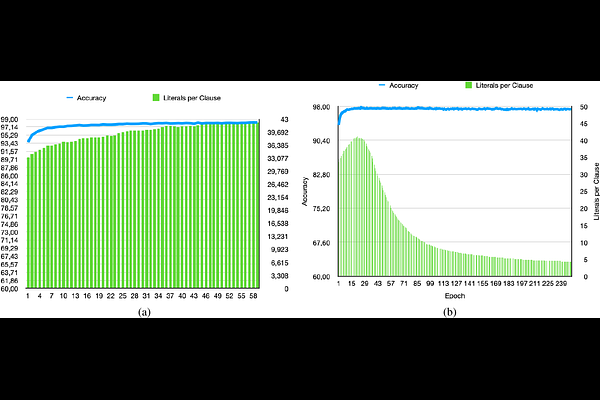
AbstractA set of variables is the Markov blanket of a random variable if it contains all the information needed for predicting the variable. If the blanket cannot be reduced without losing useful information, it is called a Markov boundary. Identifying the Markov boundary of a random variable is advantageous because all variables outside the boundary are superfluous. Hence, the Markov boundary provides an optimal feature set. However, learning the Markov boundary from data is challenging for two reasons. If one or more variables are removed from the Markov boundary, variables outside the boundary may start providing information. Conversely, variables within the boundary may stop providing information. The true role of each candidate variable is only manifesting when the Markov boundary has been identified. In this paper, we propose a new Tsetlin Machine (TM) feedback scheme that supplements Type I and Type II feedback. The scheme introduces a novel Finite State Automaton - a Context-Specific Independence Automaton. The automaton learns which features are outside the Markov boundary of the target, allowing them to be pruned from the TM during learning. We investigate the new scheme empirically, showing how it is capable of exploiting context-specific independence to find Markov boundaries. Further, we provide a theoretical analysis of convergence. Our approach thus connects the field of Bayesian networks (BN) with TMs, potentially opening up for synergies when it comes to inference and learning, including TM-produced Bayesian knowledge bases and TM-based Bayesian inference.