Single-shot Bayesian approximation for neural networks
Single-shot Bayesian approximation for neural networks
Kai Brach, Beate Sick, Oliver Dürr
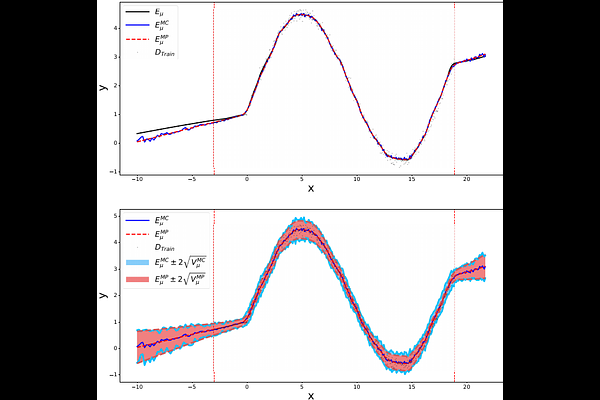
AbstractDeep neural networks (NNs) are known for their high-prediction performances. However, NNs are prone to yield unreliable predictions when encountering completely new situations without indicating their uncertainty. Bayesian variants of NNs (BNNs), such as Monte Carlo (MC) dropout BNNs, do provide uncertainty measures and simultaneously increase the prediction performance. The only disadvantage of BNNs is their higher computation time during test time because they rely on a sampling approach. Here we present a single-shot MC dropout approximation that preserves the advantages of BNNs while being as fast as NNs. Our approach is based on moment propagation (MP) and allows to analytically approximate the expected value and the variance of the MC dropout signal for commonly used layers in NNs, i.e. convolution, max pooling, dense, softmax, and dropout layers. The MP approach can convert an NN into a BNN without re-training given the NN has been trained with standard dropout. We evaluate our approach on different benchmark datasets and a simulated toy example in a classification and regression setting. We demonstrate that our single-shot MC dropout approximation resembles the point estimate and the uncertainty estimate of the predictive distribution that is achieved with an MC approach, while being fast enough for real-time deployments of BNNs. We show that using part of the saved time to combine our MP approach with deep ensemble techniques does further improve the uncertainty measures.