Discrete Denoising Diffusion Approach to Integer Factorization
Discrete Denoising Diffusion Approach to Integer Factorization
Karlis Freivalds, Emils Ozolins, Guntis Barzdins
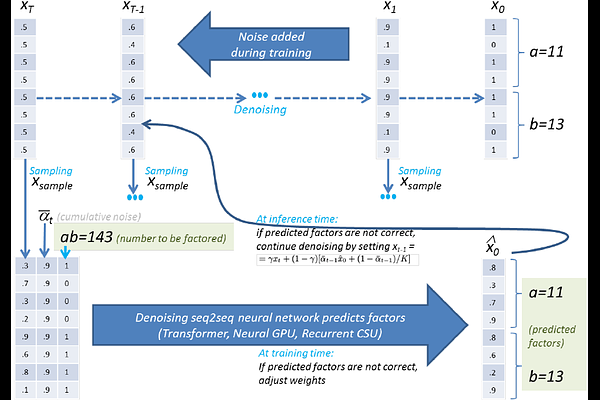
AbstractInteger factorization is a famous computational problem unknown whether being solvable in the polynomial time. With the rise of deep neural networks, it is interesting whether they can facilitate faster factorization. We present an approach to factorization utilizing deep neural networks and discrete denoising diffusion that works by iteratively correcting errors in a partially-correct solution. To this end, we develop a new seq2seq neural network architecture, employ relaxed categorical distribution and adapt the reverse diffusion process to cope better with inaccuracies in the denoising step. The approach is able to find factors for integers of up to 56 bits long. Our analysis indicates that investment in training leads to an exponential decrease of sampling steps required at inference to achieve a given success rate, thus counteracting an exponential run-time increase depending on the bit-length.