Variations and Relaxations of Normalizing Flows
Variations and Relaxations of Normalizing Flows
Keegan Kelly, Lorena Piedras, Sukrit Rao, David Roth
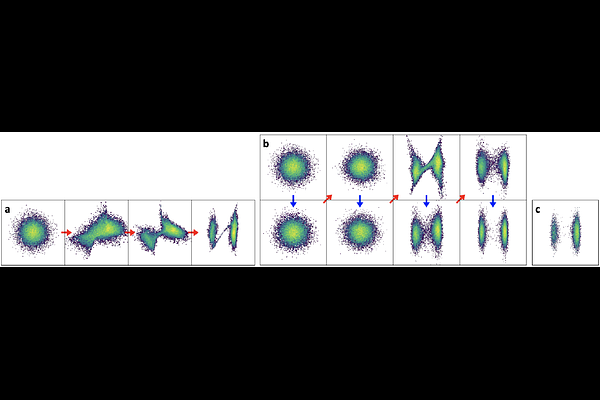
AbstractNormalizing Flows (NFs) describe a class of models that express a complex target distribution as the composition of a series of bijective transformations over a simpler base distribution. By limiting the space of candidate transformations to diffeomorphisms, NFs enjoy efficient, exact sampling and density evaluation, enabling NFs to flexibly behave as both discriminative and generative models. Their restriction to diffeomorphisms, however, enforces that input, output and all intermediary spaces share the same dimension, limiting their ability to effectively represent target distributions with complex topologies. Additionally, in cases where the prior and target distributions are not homeomorphic, Normalizing Flows can leak mass outside of the support of the target. This survey covers a selection of recent works that combine aspects of other generative model classes, such as VAEs and score-based diffusion, and in doing so loosen the strict bijectivity constraints of NFs to achieve a balance of expressivity, training speed, sample efficiency and likelihood tractability.