Thibeau Wouters, Peter T. H. Pang, Hauke Koehn, Henrik Rose, Rahul Somasundaram, Ingo Tews, Tim Dietrich, Chris Van Den Broeck

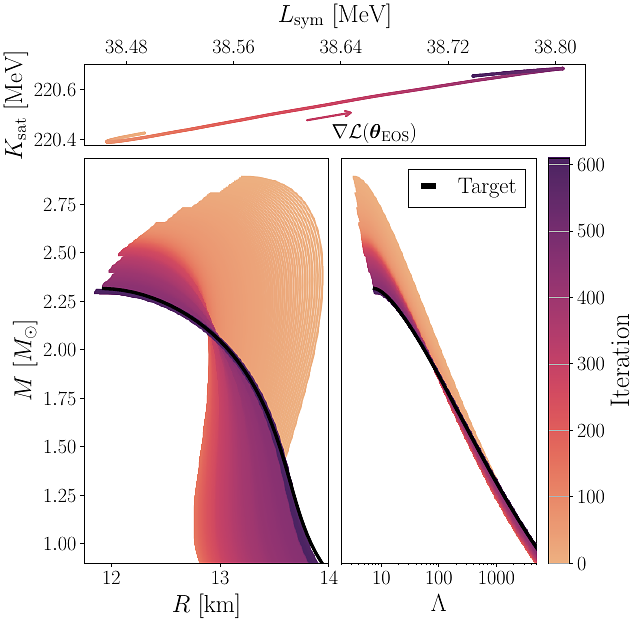
Neutron stars (NSs) probe the high-density regime of the nuclear equation of state (EOS). However, inferring the EOS from observations of NSs is a computationally challenging task. In this work, we efficiently solve this inverse problem by leveraging differential programming in two ways. First, we enable full Bayesian inference in under one hour of wall time on a GPU by using gradient-based samplers, without requiring pre-trained machine learning emulators. Moreover, we demonstrate efficient scaling to high-dimensional parameter spaces. Second, we introduce a novel gradient-based optimization scheme that recovers the EOS of a given NS mass-radius curve. We demonstrate how our framework can reveal consistencies or tensions between nuclear physics and astrophysics. First, we show how the breakdown density of a metamodel description of the EOS can be determined from NS observations. Second, we demonstrate how degeneracies in EOS modeling using nuclear empirical parameters can influence the inverse problem during gradient-based optimization. Looking ahead, our approach opens up new theoretical studies of the relation between NS properties and the EOS, while effectively tackling the data analysis challenges brought by future detectors.