VLBA astrometry of PSRs B0329+54 and B1133+16: Improved pulsar distances and comparison of global ionospheric models
VLBA astrometry of PSRs B0329+54 and B1133+16: Improved pulsar distances and comparison of global ionospheric models
Ashish Kumar, Adam T. Deller, Pankaj Jain, Javier Moldón
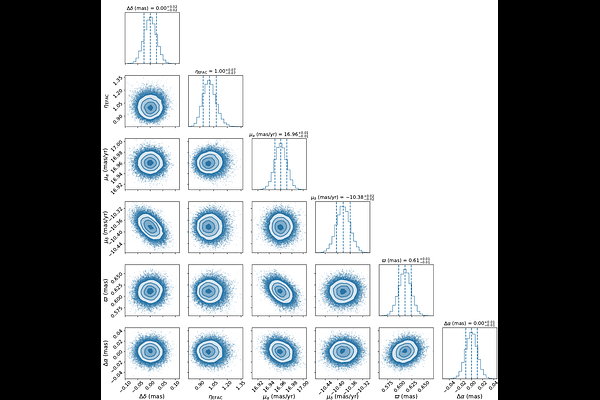
AbstractVery long baseline interferometry (VLBI) astrometry is used to determine the three-dimensional position and proper motion of astronomical objects. A typical VLBI astrometric campaign generally includes around ten observations, making it challenging to characterise systematic uncertainties. Our study on two bright pulsars, B0329+54 and B1133+16, involves analysis of broadband Very Long Baseline Array (VLBA) data over $\sim30$ epochs (spanning approximately $3.5\, {\rm years}$). This extended dataset has significantly improved the precision of the astrometric estimates of these pulsars. Our broadband study suggests that, as expected, the primary contribution to systematic uncertainties in L-band VLBI astrometry originates from the ionosphere. We have also assessed the effectiveness of the modified TEC (total electron content) mapping function, which converts vertical TEC to slant TEC, in correcting ionospheric dispersive delays using global TEC maps. The parallax and proper motion obtained from the multiple data sets, calibrated using the traditional and the modified TEC mapping functions, are consistent. However, the reduced chi-square values from least-squares fitting and precision of the fitted astrometric parameters show no significant improvement, and hence, the effectiveness of the new TEC mapping function on astrometry is unclear. For B0329+54, the refined parallax estimate is $0.611^{+0.013}_{-0.013}\, {\rm mas}$, with best-fit proper motion of $\mu_{\alpha} = 16.960^{+0.011}_{-0.010}\, {\rm mas\, yr^{-1}}$ in R.A. and and $\mu_{\delta} = -10.382^{+0.022}_{-0.022}\, {\rm mas\, yr^{-1}}$ in Dec. For B1133+16, the new estimated parallax is $2.705^{+0.009}_{-0.009}\, {\rm mas}$, with proper motions of $\mu_{\alpha} = -73.777^{+0.008}_{-0.008}\, {\rm mas\, yr^{-1}}$ and $\mu_{\delta} = 366.573^{+0.019}_{-0.019}\, {\rm mas\, yr^{-1}}$.