Fateme Jamshidi, Luca Ganassali, Negar Kiyavash

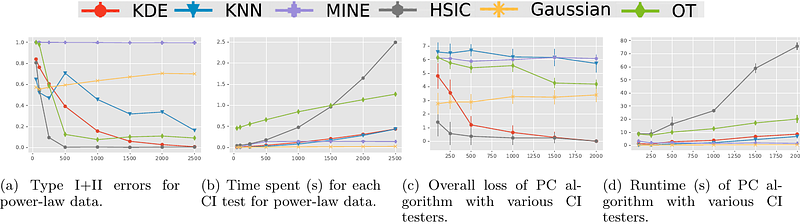
Motivated by conditional independence testing, an essential step in constraint-based causal discovery algorithms, we study the nonparametric Von Mises estimator for the entropy of multivariate distributions built on a kernel density estimator. We establish an exponential concentration inequality for this estimator. We design a test for conditional independence (CI) based on our estimator, called VM-CI, which achieves optimal parametric rates under smoothness assumptions. Leveraging the exponential concentration, we prove a tight upper bound for the overall error of VM-CI. This, in turn, allows us to characterize the sample complexity of any constraint-based causal discovery algorithm that uses VM-CI for CI tests. To the best of our knowledge, this is the first sample complexity guarantee for causal discovery for continuous variables. Furthermore, we empirically show that VM-CI outperforms other popular CI tests in terms of either time or sample complexity (or both), which translates to a better performance in structure learning as well.