Naixin Liang, Siang Peng Oh

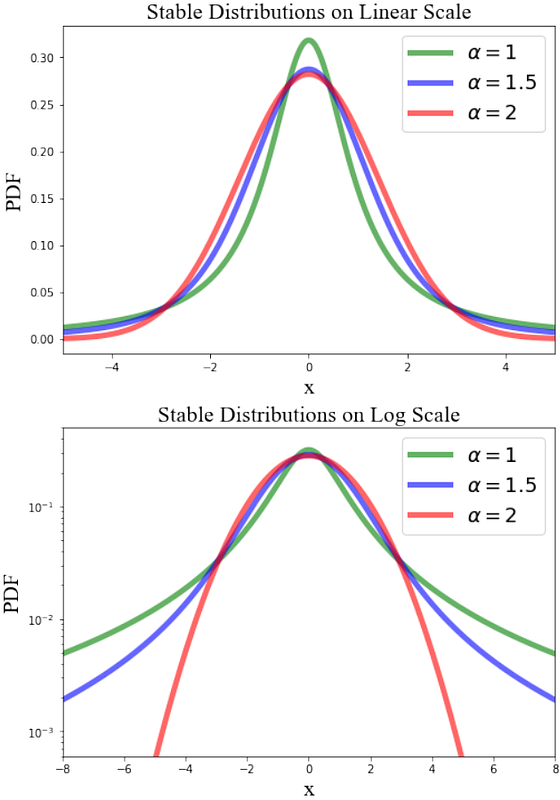
In classical diffusion, particle step-sizes have a Gaussian distribution. However, in superdiffusion, they have power-law tails, with transport dominated by rare, long L\'evy flights. Similarly, if the time interval between scattering events has power-law tails, subdiffusion occurs. Both forms of anomalous diffusion are seen in cosmic ray (CR) particle tracking simulations in turbulent magnetic fields. They also likely occur if CRs are scattered by discrete intermittent structures. Anomalous diffusion mimics a scale-dependent diffusion coefficient, with potentially wide-ranging consequences. However, the finite size of galaxies implies an upper bound on step-sizes before CRs escape. This truncation results in eventual convergence to Gaussian statistics by the central limit theorem. Using Monte-Carlo simulations, we show that this occurs in both standard finite-thickness halo models, or when CR diffusion transitions to advection or streaming-dominated regimes. While optically thick intermittent structures produce power-law trapping times and thus subdiffusion, gaussianization also eventually occurs on timescales longer than the maximum trapping time. Anomalous diffusion is a transient, and converges to standard diffusion on the (usually short) timescale of particle escape, either from confining structures (subdiffusion), or the system as a whole (superdiffusion). Thus, standard assumptions of classical diffusion are physically justified in most applications, despite growing simulation evidence for anomalous diffusion. However, if escape times are long, this is no longer true. For instance, anomalous diffusion in the CGM or ICM would change CR pressure profiles. Finally, we show the standard diagnostic for anomalous diffusion, $\langle d^2 \rangle \propto t^{\alpha}$ with $\alpha \neq 1$, is not justified for truncated L\'evy flights, and propose an alternative robust measure.