Dean Eckles, Hossein Esfandiari, Elchanan Mossel, M. Amin Rahimian

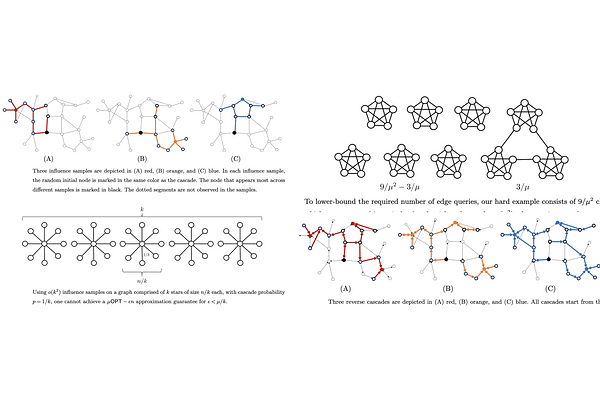
We study the task of selecting $k$ nodes, in a social network of size $n$, to seed a diffusion with maximum expected spread size, under the independent cascade model with cascade probability $p$. Most of the previous work on this problem (known as influence maximization) focuses on efficient algorithms to approximate the optimal seed set with provable guarantees given knowledge of the entire network; however, obtaining full knowledge of the network is often very costly in practice. Here we develop algorithms and guarantees for approximating the optimal seed set while bounding how much network information is collected. First, we study the achievable guarantees using a sublinear influence sample size. We provide an almost tight approximation algorithm with an additive $\epsilon n$ loss and show that the squared dependence of sample size on $k$ is asymptotically optimal when $\epsilon$ is small. We then propose a probing algorithm that queries edges from the graph and use them to find a seed set with the same almost tight approximation guarantee. We also provide a matching (up to logarithmic factors) lower-bound on the required number of edges. This algorithm is implementable in field surveys or in crawling online networks. Our probing takes $p$ as an input which may not be known in advance, and we show how to down-sample the probed edges to match the best estimate of $p$ if they are collected with a higher probability. Finally, we test our algorithms on an empirical network to quantify the tradeoff between the cost of obtaining more refined network information and the benefit of the added information for guiding improved seeding strategies.