S. Rendon Restrepo, T. Rometsch, U. Ziegler, O. Gressel

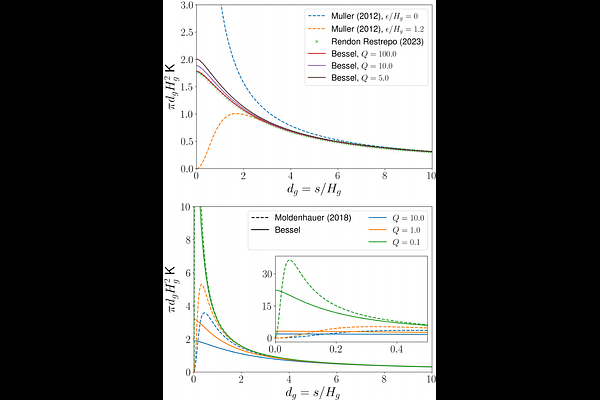
Planet-forming discs often contain structures like spiral arms, typically linked to the disc's gravitational forces. In 2D models, an ad hoc softening prescription is commonly used for self-gravity, but this overlooks the vertical structure's impact, suppresses the Newtonian nature of gravity at short distances and doesn't respect Newton's third law. To address these issues, associated with a Plummer potential approximation, we developed an exact self-gravity kernel for thin, hydrostatically supported discs, including a dust fluid component. Our analytical framework provides a precise 2D self-gravity prescription validated by benchmarks and 2D/3D numerical tests. The derived kernel, based on modified Bessel functions, maintains Newtonian gravitation features, such as point-wise symmetry, a smooth transition from light to massive discs and a singularity at zero distance, among others. In contrast to other prescriptions found in the literature, it proves capable of leading to an additional, and previously unnoticed, source of gravitational runaway discernible only at infinitesimal distances. We finally note that our new prescription remains compatible with methods based on the fast Fourier transform, affording superior computational efficiency. Our exact kernel formulation overcomes substantial limitations inherent in the smoothing-length approach. It permits a novel, fully consistent treatment of self-gravity in Gaussian-stratified thin discs. The approach, that makes the usage of the Plummer potential obsolete, will prove useful to studying all common planet formation scenarios, which are often backed by 2D-flat numerical simulations. Accordingly, in an accompanying paper, we will investigate how the occurence of the gravitational instability is affected.