Robust Single Rotation Averaging Revisited
Robust Single Rotation Averaging Revisited
Seong Hun Lee, Javier Civera
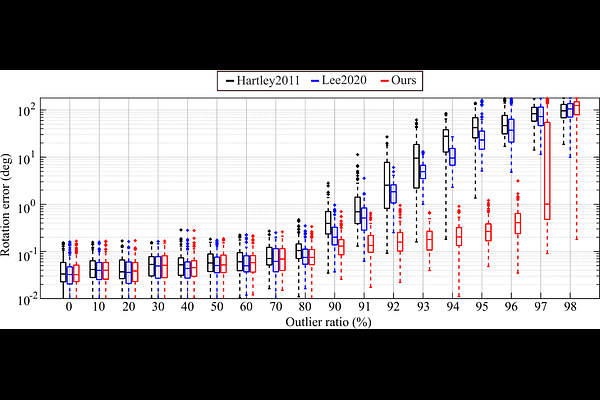
AbstractIn this work, we propose a novel method for robust single rotation averaging that can efficiently handle an extremely large fraction of outliers. Our approach is to minimize the total truncated least unsquared deviations (TLUD) cost of geodesic distances. The proposed algorithm consists of three steps: First, we consider each input rotation as a potential initial solution and choose the one that yields the least sum of truncated chordal deviations. Next, we obtain the inlier set using the initial solution and compute its chordal $L_2$-mean. Finally, starting from this estimate, we iteratively compute the geodesic $L_1$-mean of the inliers using the Weiszfeld algorithm on $SO(3)$. An extensive evaluation shows that our method is robust against up to 99% outliers given a sufficient number of accurate inliers, outperforming the current state of the art.