Michael Weiler

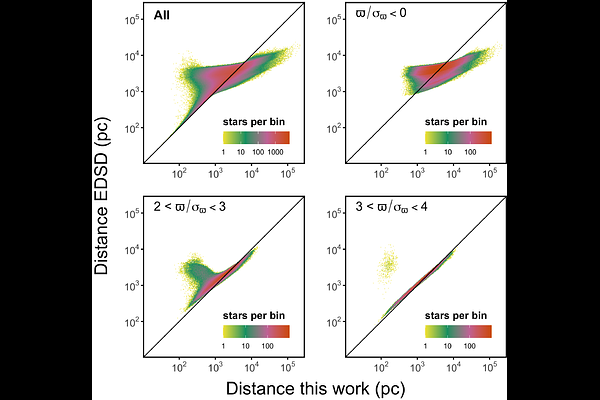
The computation of magnitudes and distances from low signal-to-noise observations is known to be problematic, in the sense that the magnitudes and distances tend to assume extreme values, or are even undefined or unphysical in the case of negative observed fluxes or parallaxes. In this work we show that magnitudes can be computed consistently at all signal-to-noise levels, and even for negative fluxes, if the prior information that the true flux or distance is non-negative is properly included. Furthermore, we derive an all-purpose estimator for distances from a prior implementing only the non-negativity of the true parallax. We apply our results to the case of combining magnitudes to colours, and magnitudes and distances to obtain absolute magnitudes. The resulting expressions are easy to compute and we show that the resulting distribution functions for magnitudes, colours, distances, and absolute magnitudes are not only consistent for all signal-to-noise levels and applicable to both, positive and negative observed fluxes and parallaxes, but also show no strong tails. While biases at very low signal-to-noise levels are unavoidable, the estimator for distances derived in this work is less biased than previously used estimators. We find that the magnitude, colour, distance, and absolute magnitude distributions for vanishing signals converge to limiting distributions, whose median values are important for assessing biases when working with data at low signal-to-noise levels.