Xiaoshan Huang, Itai Linial, Yan-Fei Jiang

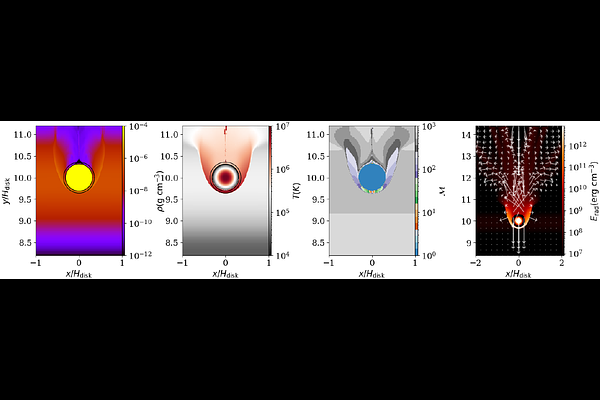
We perform two-dimensional, multi-group radiation hydrodynamic simulations to explore the observational properties of a solar-like star colliding with an accretion disk around a supermassive black hole at separation of $\sim 100$ gravitational radii. We find that the star-disk collision produces ejecta on both sides of the disk. As the ejecta expand and cool, transient flares arise, reaching peak bolometric luminosity of up to $L\gtrsim10^{43}\rm erg~s^{-1}$. We estimate that the typical light curve rises and decays on an hour timescale. The spectral energy distribution (SED) peaks in $20-50$eV. The optical depth in soft X-rays is lower than the frequency-integrated optical depth, yielding $100$eV-$1$KeV luminosity $\nu L_{\nu}\gtrsim10^{42}\rm erg~s^{-1}$. The ejecta aligned with the star's incident direction shows breakout emission, leading to asymmetric SED evolution of the two ejecta. The SED evolution is roughly consistent with those seen in short-period quasi-periodic eruptions (QPEs), which have eruption duration ranging from sub-hour to hours, but the ejecta cooling emission alone may not be sufficient to explain the longer duration flares. Increasing incident velocity generally produces a brighter and harder flare. A larger disk scale height prolongs the breakout emission but leads to a somewhat softer SED. A higher disk surface density can lead to higher ejecta temperature, reducing bound-free opacity and increasing luminosity. When lowering the disk surface density, we find that the ejecta becomes optically thin when the scattering optical depth across disk is at the order of $\tau_{\rm disk}\sim200$, and the ejecta disappear when $\tau_{\rm disk}\sim10$.