On the latent dimension of deep autoencoders for reduced order modeling of PDEs parametrized by random fields
On the latent dimension of deep autoencoders for reduced order modeling of PDEs parametrized by random fields
Nicola Rares Franco, Daniel Fraulin, Andrea Manzoni, Paolo Zunino
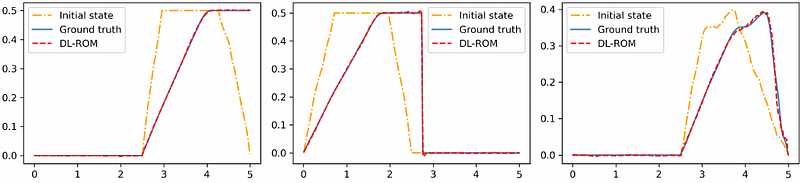
AbstractDeep Learning is having a remarkable impact on the design of Reduced Order Models (ROMs) for Partial Differential Equations (PDEs), where it is exploited as a powerful tool for tackling complex problems for which classical methods might fail. In this respect, deep autoencoders play a fundamental role, as they provide an extremely flexible tool for reducing the dimensionality of a given problem by leveraging on the nonlinear capabilities of neural networks. Indeed, starting from this paradigm, several successful approaches have already been developed, which are here referred to as Deep Learning-based ROMs (DL-ROMs). Nevertheless, when it comes to stochastic problems parameterized by random fields, the current understanding of DL-ROMs is mostly based on empirical evidence: in fact, their theoretical analysis is currently limited to the case of PDEs depending on a finite number of (deterministic) parameters. The purpose of this work is to extend the existing literature by providing some theoretical insights about the use of DL-ROMs in the presence of stochasticity generated by random fields. In particular, we derive explicit error bounds that can guide domain practitioners when choosing the latent dimension of deep autoencoders. We evaluate the practical usefulness of our theory by means of numerical experiments, showing how our analysis can significantly impact the performance of DL-ROMs.